19. (1)已知$m= 1 + 2n$,求代数式$7m - 14n$的值;
(2)已知$m - 2n= 1$,求代数式$3 + 7m - [9n + 5(m - n)]$的值.
答案:(1)7(2)5
解析:
(1)因为$m = 1 + 2n$,所以$m - 2n = 1$,则$7m - 14n = 7(m - 2n) = 7×1 = 7$
(2)$3 + 7m - [9n + 5(m - n)] = 3 + 7m - (9n + 5m - 5n) = 3 + 7m - (4n + 5m) = 3 + 7m - 4n - 5m = 3 + 2m - 4n = 3 + 2(m - 2n)$,因为$m - 2n = 1$,所以原式$= 3 + 2×1 = 5$
20. 已知多项式$x^2 + ax - y + b与bx^2 - 3x + 6y - 3的差的值与字母x$的取值无关,求代数式$3(a^2 - 2ab - b^2) - (4a^2 + ab + b^2)$的值.
答案:$a=-3$,$b=1$,原式$=8$
解析:
$(x^2 + ax - y + b)-(bx^2 - 3x + 6y - 3)$
$=x^2 + ax - y + b - bx^2 + 3x - 6y + 3$
$=(1 - b)x^2 + (a + 3)x - 7y + (b + 3)$
因为差的值与字母$x$的取值无关,所以$1 - b = 0$且$a + 3 = 0$,解得$b = 1$,$a = -3$。
$3(a^2 - 2ab - b^2)-(4a^2 + ab + b^2)$
$=3a^2 - 6ab - 3b^2 - 4a^2 - ab - b^2$
$=-a^2 - 7ab - 4b^2$
当$a = -3$,$b = 1$时,
原式$=-(-3)^2 - 7×(-3)×1 - 4×1^2$
$=-9 + 21 - 4$
$=8$
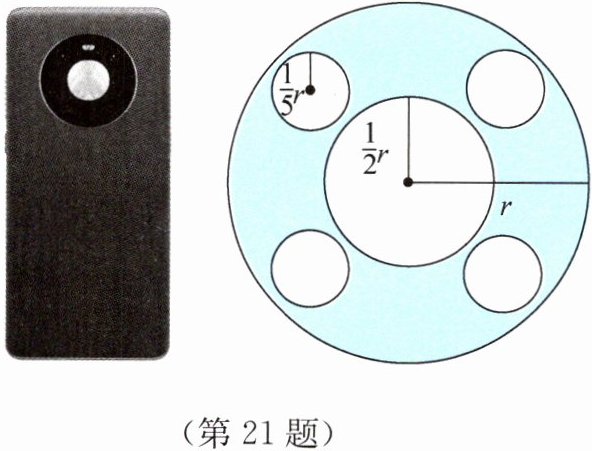
21. 某款手机后置摄像头模组如图所示. 其中,大圆的半径为$r$,中间小圆的半径为$\frac{1}{2}r$,4个半径为$\frac{1}{5}r$的高清圆形镜头分布在两圆之间.
(1)请用含$r$的代数式表示图中阴影部分的面积;
(2)当$r= 2$cm时,求图中阴影部分的面积($\pi$取3).
答案:(1)$\frac{59}{100}\pi r^{2}\ cm^{2}$ (2)$\frac{177}{25}\ cm^{2}$
解析:
(1)阴影部分面积 = 大圆面积 - 中间小圆面积 - 4个高清圆形镜头面积
大圆面积:$\pi r^2$
中间小圆面积:$\pi \left(\frac{1}{2}r\right)^2 = \frac{1}{4}\pi r^2$
1个高清圆形镜头面积:$\pi \left(\frac{1}{5}r\right)^2 = \frac{1}{25}\pi r^2$,4个面积:$4 × \frac{1}{25}\pi r^2 = \frac{4}{25}\pi r^2$
阴影部分面积:$\pi r^2 - \frac{1}{4}\pi r^2 - \frac{4}{25}\pi r^2 = \left(1 - \frac{25}{100} - \frac{16}{100}\right)\pi r^2 = \frac{59}{100}\pi r^2$
(2)当$r=2\ cm$,$\pi=3$时
阴影部分面积:$\frac{59}{100} × 3 × (2)^2 = \frac{59}{100} × 3 × 4 = \frac{177}{25}\ cm^2$
(1)$\frac{59}{100}\pi r^{2}$
(2)$\frac{177}{25}$