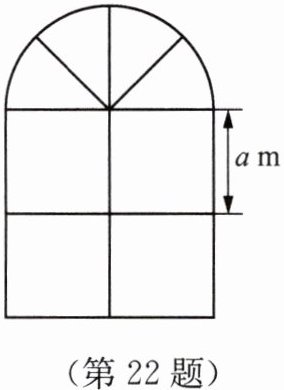
22. 工程师为某建筑制定装修方案,其中有一扇窗户的形状如图所示,上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长是$a$m,图中窗框均为塑钢材质,已知整个窗户的外框部分为A型塑钢材质,里面的窗框为B型塑钢材质,其余部分都是透光玻璃($\pi$取3).
(1)用含$a$的代数式表示这个窗户的透光面积(窗框部分忽略不计).
(2)如果$a= 0.5$,A型塑钢材质价格为250元/m,B型塑钢材质价格为180元/m,玻璃价格为40元/m^2,现有甲、乙两个公司作为选择,其中,甲公司的收费方式为每满500元可以减60元;乙公司的收费方式为如果总价超过1000元,那么总价打9折. 如何选择可以使总花费最少?
答案:(1)窗户的面积$=4a^{2}+\frac{1}{2}\pi a^{2}=\left(4+\frac{1}{2}\pi\right)a^{2}=5.5\ a^{2}(m^{2})$ (2)图形外部周长为$\frac{1}{2}×2\pi a+6a=9a=4.5(m)$,内部材料长为$9a=4.5(m)$,A型塑钢材质为250元/$m^{2}$,B型塑钢材质180元/$m^{2}$,玻璃价格为40元/$m^{2}$,所以总价为$250×4.5+4.5×180+5.5×0.5^{2}×40=1\ 990(元)$,选择甲公司需付:$1\ 990-3×60=1\ 810(元)$,选择乙公司需付:$1\ 990×0.9=1\ 791(元)$,所以选择乙公司便宜
解析:
(1)窗户的透光面积为下部四个小正方形面积与上部半圆形面积之和。下部四个小正方形的面积为$4a^2$,上部半圆形的半径为$a$,面积为$\frac{1}{2}\pi a^2$。因为$\pi = 3$,所以透光面积为$4a^2+\frac{1}{2}×3× a^2 = 4a^2+\frac{3}{2}a^2=\frac{11}{2}a^2 = 5.5a^2\ m^2$。
(2)当$a = 0.5$时:
透光面积为$5.5×(0.5)^2=5.5×0.25 = 1.375\ m^2$,玻璃费用为$1.375×40=55$元。
A型塑钢材质为外框部分,其长度为半圆的弧长加上下部正方形组合图形的外部边长。半圆的弧长为$\frac{1}{2}×2\pi a=\pi a$,下部外部边长为$6a$,所以A型塑钢长度为$\pi a + 6a$,因为$\pi = 3$,所以长度为$3a+6a = 9a$,即$9×0.5 = 4.5\ m$,费用为$4.5×250 = 1125$元。
B型塑钢材质为内部窗框,长度为$9a$,即$4.5\ m$,费用为$4.5×180 = 810$元。
总费用为$1125+810 + 55=1990$元。
甲公司收费:每满500元减60元,$1990÷500 = 3\cdots\cdots490$,可减$3×60 = 180$元,需付$1990-180 = 1810$元。
乙公司收费:总价超过1000元打9折,需付$1990×0.9 = 1791$元。
因为$1791<1810$,所以选择乙公司总花费最少。