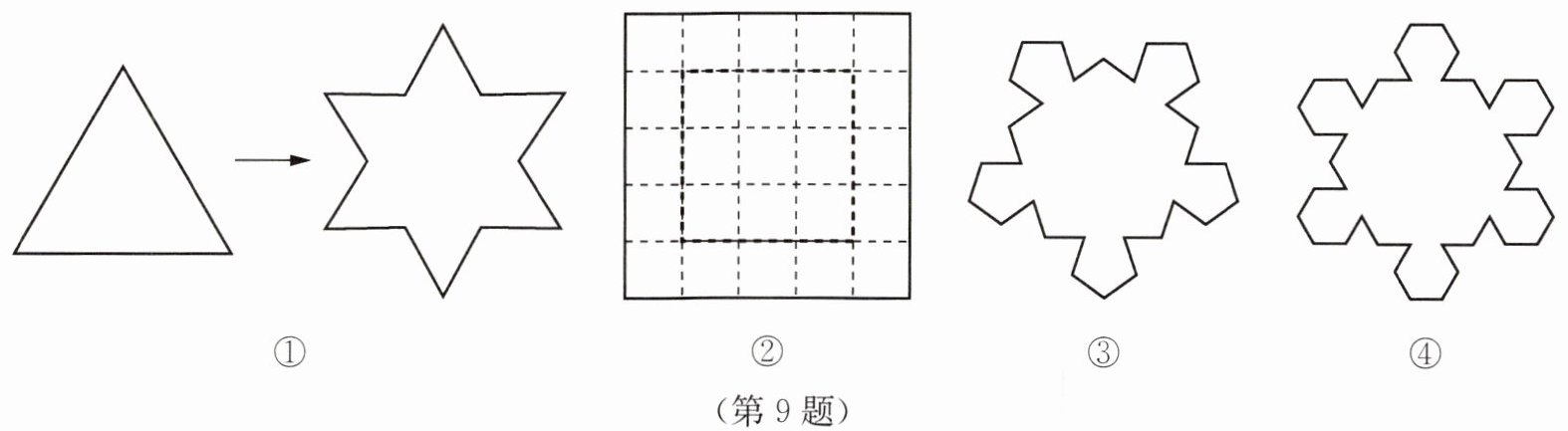
9. 我们把正n边形(n≥3)的各边三等分,分别以居中的那条线段为一边向外作正n边形,并去掉居中的那条线段,得到一个新的图形,叫作正n边形的“扩展图形”,并将它的边数记为aₙ.如图①,将正三角形进行上述操作后得到其“扩展图形”,且a_3= 12.图③、图④分别是正五边形,正六边形的“扩展图形”.
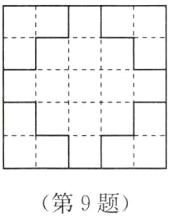
(1) 如图②,在5×5的正方形网格中有一个用粗虚线画的正方形,请在图②中用实线画出此正方形的“扩展图形”;
(2) 已知a_3= 12,a_4= 20,a_5= 30,则图④中a_6= ______,根据以上规律,正n边形的“扩展图形”中aₙ= ______(用含n的式子表示);
(3) 已知$\frac{1}{a_3}= \frac{1}{3}-\frac{1}{4}$,$\frac{1}{a_4}= \frac{1}{4}-\frac{1}{5}$,$\frac{1}{a_5}= \frac{1}{5}-\frac{1}{6}$,…,且$\frac{1}{a_3}+\frac{1}{a_4}+\frac{1}{a_5}+\dots +\frac{1}{a_n}= \frac{97}{300}$,则n= ______.
答案:(1)如图所示
(2)42,$n(n+1)$.提示:图④中$a_{6}=6×7=42$,根据以上规律,正n边形的“扩展图形”中$a_{n}=n(n+1)$
(3)因为$\frac{1}{a_{3}}=\frac{1}{3}-\frac{1}{4}$,$\frac{1}{a_{4}}=\frac{1}{4}-\frac{1}{5}$,$\frac{1}{a_{5}}=\frac{1}{5}-\frac{1}{6}$,$\cdots$,且$\frac{1}{a_{3}}+\frac{1}{a_{4}}+\frac{1}{a_{5}}+\cdots+\frac{1}{a_{n}}=\frac{97}{300}$,所以$\frac{1}{3}-\frac{1}{n+1}=\frac{97}{300}$,解得$n=99$