跟踪练习$1$
(新素养推理意识)在$□$里填合适数字:
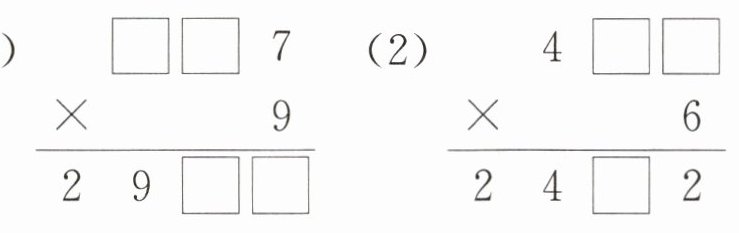
答案: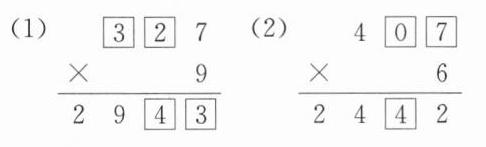
例$2$观察前四道算式规律,写出后两道得数:
$999×1 = 999$ $999×2= 1998$ $999×3= 2997$ $999×4= 3996$ $999×5= (
4995
)$ $999×6= (
5994
)$
思路分析发现:乘数$999$乘连续自然数,得数是四位数且百位十位为$9$,千位个位是“$9$”与乘数积的十位个位数字。
规范解答$4995$ $5994$
技巧归纳解决规律问题要先观察不变与变化部分及变化规律。
答案:解析:本题考查的是寻找算式的规律来解决问题。
积的变化规律是:一个因数不变,另一个因数扩大或缩小若干倍,积也扩大或缩小相同的倍数。
首先,观察给出的算式:
$999 × 1 = 999$
$999 × 2 = 1998$
$999 × 3 = 2997$
$999 × 4 = 3996$
可以发现,当999乘以一个连续的自然数时,得到的结果是一个四位数,其中千位和个位数字组成的数与乘数(即那个连续的自然数)有关,具体地说,就是它们相乘的结果的十位和个位数字。
同时,还注意到结果中的百位和十位数字始终是99。
基于这个观察,可以推断出:
$999 × 5$ 的结果应该是4995,因为 $5 × 9 = 45$,取个位和十位数字作为结果的千位和个位,百位和十位保持为99。
同理,$999 × 6$ 的结果应该是5994,因为 $6 × 9 = 54$。
答案:$4995$;$5994$。
跟踪练习$2$按规律写算式:
$1×8 +1= 9$ $12×8 +2= 98$ $123×8 +3= 987$
1234×8+4=9876
12345×8+5=98765
答案:答案不唯一,如:1234×8+4=9876 12345×8+5=98765
解析:
1234×8+4=9876
12345×8+5=98765