例$3$用火柴棒摆平行四边形:
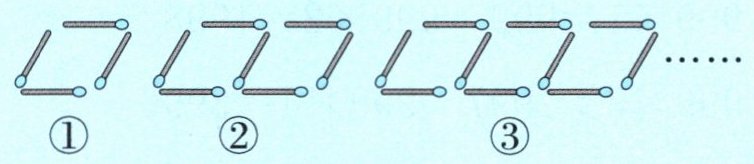
(1)摆第$33$个图形用多少根火柴棒?
(2)$22$根火柴棒能摆成第几个图形?
思路分析摆第$1个用4$根,第$2个用7$根,第$3个用10$根……每多摆$1个多3$根,规律为“图形编号$×3 +1= $火柴棒根数”。
规范解答(1)$33×3 +1 = 100$(根)
答:一共要用$100$根火柴棒。
(2)$22 -1 = 21$(根)$21÷3 = 7$(个)
答:能摆成第$7$个图形。
技巧归纳先找“图形编号”和“火柴棒根数”规律并表示为数量关系式再解题。
答案:
(1) $33×3 + 1$
$= 99 + 1$
$ = 100$(根)
答:一共要用$100$根火柴棒。
(2) $22 - 1 = 21$(根)
$21÷3 = 7$(个)
答:能摆成第$7$个图形。
跟踪练习$3$(新趋势推导探究)摆$1个三角形要3$根火柴棒,摆$2个要5$根(如图),摆$120$个要(
241
)根,现有$19$根可摆(
9
)个这样的三角形。
(三角形图形示意)

答案:241 9
解析:
摆1个三角形要3根火柴棒,摆2个三角形要5根火柴棒,观察规律可得:摆$n$个三角形需要$2n + 1$根火柴棒。
当$n = 120$时,$2×120 + 1 = 241$根。
现有19根火柴棒,设可摆$m$个三角形,则$2m + 1 = 19$,解得$m = 9$。
241 9
例$1欢欢和乐乐共有邮票88$枚,乐乐的邮票枚数是欢欢的$3$倍。两人各有多少枚邮票?
思路分析画线段图:
(欢欢乐乐邮票线段图)

把欢欢邮票数看作$1$倍数,乐乐是$3$倍数,总数是$4$倍数。
规范解答$1 +3 = 4$ 欢欢:$88÷4 = 22$(枚)
乐乐:$22×3 = 66$(枚)
答:欢欢有$22$枚,乐乐有$66$枚。
技巧归纳解决和倍问题要找准“和”与“倍数”,用和除以倍数和得$1$倍数,再求几倍数。
答案:解析:本题考查和倍问题,通过线段图分析数量关系,利用倍数关系求出两人各自邮票的数量。
已知乐乐的邮票枚数是欢欢的$3$倍,把欢欢邮票数看作$1$倍数,乐乐是$3$倍数,那么两人邮票总数就是$1 + 3 = 4$倍数。
因为两人共有邮票$88$枚,用总数除以倍数和$4$,就可以得到$1$倍数,即欢欢的邮票数,再根据倍数关系求出乐乐的邮票数。
答案:欢欢和乐乐邮票数倍数和:$1 + 3 = 4$。
欢欢的邮票数:$88÷4 = 22$(枚)。
乐乐的邮票数:$22×3 = 66$(枚)。
答:欢欢有$22$枚邮票,乐乐有$66$枚邮票。