1. 填空。
(1) 我们班有男生18人,女生15人,男生人数是女生人数的$\frac{
6
}{
5
}$,女生人数是男生人数的$\frac{
5
}{
6
}$,男生人数约占全班总人数的(
54.5
)%,女生人数约占全班总人数的(
45.5
)%。
(2) 《安徽省义务教育阶段学校办学基本标准》中规定:中小学校园绿地率不得低于35%。某小学的占地面积约30000平方米,要想绿地率达标,至少需要(
10500
)平方米的绿地。
答案:(1)$\frac{6}{5}$ $\frac{5}{6}$ 54.5 45.5
【点拨】$18÷15=\frac{6}{5}$,$15÷18=\frac{5}{6}$,$18÷(18+15)\approx54.5\%$,$15÷(18+15)\approx45.5\%$。
(2)10500
【点拨】把学校的总面积看作单位“1”,求绿地面积至少是多少,就相当于求30000平方米的35%是多少,用乘法解答。
2. 下面是一个长方体盒子的展开图,长方体盒子的表面积和体积各是多少?
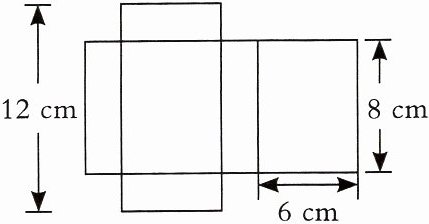
答案:$(12-8)÷2=2$(cm)
表面积:$(6×8+6×2+8×2)×2=152$($\text{cm}^2$)
体积:$6×8×2=96$($\text{cm}^3$)
答:长方体盒子的表面积是$152\text{cm}^2$,体积是$96\text{cm}^3$。
【点拨】先根据题图求出长方体的高,再根据长方体的表面积和体积计算公式解答。
3. 大扫除啦!同学们干得热火朝天,有人负责扫地、有人负责擦玻璃……典典、龙龙和聪聪负责在教室里擦桌椅,一共有52套桌椅,典典擦的比龙龙少2套,聪聪比龙龙多擦了3套,他们三人分别擦了多少套桌椅?
答案:$(52+2-3)÷3=17$(套)
$17-2=15$(套) $17+3=20$(套)
答:龙龙擦了17套桌椅,典典擦了15套桌椅,聪聪了擦20套桌椅。
【点拨】根据典典擦的比龙龙少2套,聪聪比龙龙多擦了3套,可知龙龙擦的套数的3倍是$(52+2-3)$套;据此求出龙龙擦的套数,从而可求出其余2人分别擦了多少套。
4. 新情境·图表信息 一个工厂有三个车间,已知第一车间有36人,并且人数最多。有以下三条关于车间人数的信息(含有准确信息):
A. 第一车间的人数占三个车间总人数的30%;
B. 第一车间的人数比三个车间总人数的$\frac{2}{5}$少6人;
C. 第一、第二、第三车间的人数比是4:2:3。
(1) 以上三条信息中,准确的信息是(
C
)。
(2) 根据准确的这条信息算一算,这个工厂三个车间一共有多少人?
$36÷4×(4+2+3)=81$(人)
答:这个工厂三个车间一共有81人。
答案:(1)C
【点拨】由信息A可计算出总人数为$36÷30\%=120$(人),另外两个车间的总人数为$120-36=84$(人),可知另外两个车间人数不论怎么分配,至少有一个车间人数会超过36人,所以信息A不准确;由信息B可计算出总人数为$(36+6)÷\frac{2}{5}=105$(人),另外两个车间总人数为$105-36=69$(人),也不能保证第一车间的人数最多,所以信息B也不准确;由信息C可看出第一车间的人数最多,因此信息C是准确的。
(2)$36÷4×(4+2+3)=81$(人)
答:这个工厂三个车间一共有81人。
5. 新题型·探究题 手工课上,典典、华华、梦梦都用边长12cm的正方形硬纸板剪折成无盖的长方体纸盒,三个人都是先剪掉四个角上的小正方形(如图,同一个图中的四个小正方形的边长相同),算一算三人做出的纸盒的容积,比一比谁做出的纸盒的容积最大。(硬纸板的厚度忽略不计)
(单位:cm)

答案:典典:$12-3×2=6$(cm) $6×6×3=108$($\text{cm}^3$)
华华:$12-2×2=8$(cm) $8×8×2=128$($\text{cm}^3$)
梦梦:$12-1×2=10$(cm) $10×10×1=100$($\text{cm}^3$)
$128>108>100$
答:典典做出的纸盒的容积是$108\text{cm}^3$,华华做出的纸盒的容积是$128\text{cm}^3$,梦梦做出的纸盒的容积是$100\text{cm}^3$,华华做出的纸盒的容积最大。
【点拨】先明确三人做出的纸盒的长、宽、高,再计算出各自的容积,然后比较大小。