1. ☆【湖州市】如图,瓶中容纳了(
C
)是550mL的饮料。
A.质量
B.面积
C.体积
D.容积
答案:C
2. ☆【许昌市】对于“汽车油箱中加满油是55L”这句话,下面说法错误的是(
B
)。
A.油箱的容积是55L
B.油箱中油的质量是55L
C.油箱中油的体积是$55dm^3$
D.油箱的体积大于$55dm^3$
答案:B [点拨]油箱中容纳油的体积就是油箱的容积,故选项A正确;L是容器容积和液体体积单位,不是质量单位,故选项B错误;选项C油箱中油的体积是55dm³是正确的;油箱的体积大于它的容积,故选项D是正确的。
3. ☆☆【太原市】如图,一个正方体的展开图,6个面上分别写着礼、乐、射、御、书、数(中国古代“六艺”)。
(1)涂一涂,写一写,把这个展开图补充完整。
(2)与“御”相对的是( )。

答案:(1)(答案不唯一)

(2)礼
4. ☆☆【徐州市】一个长方体火柴盒(如图)。亮亮画了这个火柴盒的内盒展开图(每个小方格代表1平方厘米),但是他却不会画火柴盒的外盒展开图,你来帮帮他,在方格纸上画出外盒的展开图,并填空。(外盒有4个面,硬纸板的厚度忽略不计)
算一算:这个火柴盒的体积是( )立方厘米。

答案: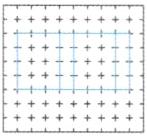
12 [点拨]由内盒展开图可知,火柴盒的长是4厘米,宽是3厘米,高是1厘米。
5. ☆☆【南京市】一名设计师制作一个长方体铝合金框架,如下图,估算一下,他大约用去(
B
)铝合金条。

A.12米
B.5米
C.$\frac {5}{4}$米
D.6米
答案:B [点拨]这个长方体的一条长与一条宽的和接近1米,则所有长与宽的和接近4米,一条高接近$\frac{1}{4}$米,所以4条高的和接近1米,由此得出这个长方体的棱长和接近5米。
6. ☆☆☆【平顶山市】一根细铁丝长48厘米,围成一个长、宽、高的比是3:2:1的长方体,该长方体的表面积是(
88
)平方厘米;如果改围成正方体,体积会增加(
16
)立方厘米。
答案:88 16
[点拨]根据长方体的各棱长特征以及按比分配,可求出长方体的长是$48÷ 4× \frac{3}{3+2+1}=6$(厘米),宽是$48÷ 4× \frac{2}{3+2+1}=4$(厘米),高是$48÷ 4× \frac{1}{3+2+1}=2$(厘米),长方体的表面积=(6×4+6×2+4×2)×2=88(平方厘米);长方体的体积=6×4×2=48(立方厘米),改围成正方体的棱长=48÷12=4(厘米),则正方体的体积=$4^{3}=64$(立方厘米),体积增加64 - 48=16(立方厘米)。
7. ☆☆☆【滁州市】从长、宽、高分别为15cm、12cm、10cm的长方体中截取棱长为3cm的正方体(截取时损耗不计),最多可以截取多少个这样的正方体,还剩多少立方厘米?
答案:15÷3=5(个) 12÷3=4(个)
10÷3≈3(个) 5×4×3=60(个)
$15× 12× 10-{3}^{3}× 60=180\left(\mathrm{c}{\mathrm{m}}^{3}\right)$
答:最多可以截取60个这样的正方体,还剩180cm³。
[点拨]用长方体的长、宽和高分别除以小正方体的棱长,即可求出沿一条长、一条宽、一条高分别可以截取几个正方体,相乘即可求出最多可以截取多少个这样的正方体,再用长方体的体积减去截取的正方体的体积和,即可求出还剩的体积。
8. ☆☆【南京市】如下图,两个立体图形都是由棱长为1厘米的正方体搭成的,①号立体图形的表面积可以这样算:$(4+6+4)×2$,其中4、6、4分别是从前面、上面和右面观察到的图形的面积,用①号立体图形表面积的求法,求②号立体图形表面积可以列式为
(5+6+4)×2
(只列式不计算)。

答案:(5+6+4)×2 [点拨]先明确从前面、上面、右面观察到的图形的面积,再列式。
9. ☆☆【洛阳市】魔方又叫鲁比克方块,是一款风靡全球的益智玩具。天天是魔方爱好者,他有一款三阶魔方,即$3×3×3$。可是一次玩耍中,不小心掉了一个小正方体,魔方的表面积会(
D
)。
A.变大
B.变小
C.不变
D.答案不唯一
答案:D [点拨]根据题意可以分三种情况:第一种情况:如果掉的小正方体是魔方的8个顶点中的一处,会减少三个小正方形的面积,同时会增加三个小正方形的面积,那么魔方的表面积不变;第二种情况:掉的小正方体是魔方一条棱上非顶点位置的一处,会减少两个小正方形的面积,但同时会增加四个小正方形的面积,那么魔方的表面积变大;第三种情况:掉的小正方体在魔方每个面的中心位置,会减少一个小正方形的面积,但同时会增加五个小正方形的面积,那么魔方的表面积变大。综上可知,魔方的表面积可能变大也可能不变,即答案不唯一。
10. ☆☆☆【太原市】甲图是由1立方厘米的小正方体堆成的一个大长方体,把甲图推倒后,再利用这一堆小正方体在乙图这样的“地基”上往上堆成一栋“大楼”。这栋“大楼”有多少层?(地基中的每个小正方形恰好与每个小正方体的一个面相同,要求这栋“大楼”每一层都有4个小正方体)
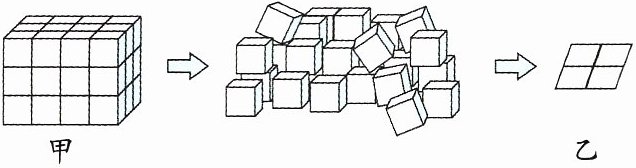
答案:4×3×3=36(个) 36÷(2×2)=9(层)
答:这栋“大楼”有9层。
[点拨]从甲图可以看出一共有4×3×3=36(个)小正方体,所以这栋“大楼”有36÷4=9(层)。