1. 算一算,填一填。
$\frac{7}{8} × \frac{8}{7} =$
1
$\frac{1}{5} × 5 =$
1
$\frac{11}{6} × \frac{6}{11} =$
1
$0.25 × 4 =$
1
$1 \frac{1}{2} × \frac{2}{3} =$
1
$0.125 × 8 =$
1
像上面的算式那样,乘积是(
1
)的两个数互为倒数。
答案:1 1 1 1 1 1 1
$\frac{7}{6} \xrightarrow[\text{交换位置}]{7 \text{和} 6} \frac{
6
}{
7
}$
$2.5 = \frac{
5
}{
2
} \xrightarrow[\text{交换位置}]{
5和2
} \frac{
2
}{
5
}$
$1 \frac{3}{5} = \frac{
8
}{
5
} \xrightarrow[\text{交换位置}]{
8和5
} \frac{
5
}{
8
}$
答案:$\frac{6}{7}$ $\frac{5}{2}$ 5和2 $\frac{2}{5}$ $\frac{8}{5}$ 8和5 $\frac{5}{8}$
3. 下列说法错误的是(
C
)。
① 1 的倒数是 1,0 没有倒数。
② 因为 0 乘任何数都不等于 1 且 0 不能作除数,所以 0 没有倒数。
③ 0 的倒数是 0。
A.①②
B.②
C.③
D.②③
答案:C
4. 写出下面各数的倒数。
$\frac{4}{7}$(
$\frac{7}{4}$
) $1 \frac{8}{9}$(
$\frac{9}{17}$
) 10(
$\frac{1}{10}$
)
0.75(
$\frac{4}{3}$
) 1.4(
$\frac{5}{7}$
) 1(
1
)
我发现:当 $a$ 为(
1
)时,它的倒数是它本身;当 $a$ 为(
真分数
)时,它的倒数大于 $a$;当 $a$ 为(
0
)时,它没有倒数;当 $a$ 为(
假分数
)时,它的倒数小于或等于 $a$。(填“0”“1”“真分数”或“假分数”)
答案:$\frac{7}{4}$ $\frac{9}{17}$ $\frac{1}{10}$ $\frac{4}{3}$ $\frac{5}{7}$ 1 1 真分数 0 假分数
(1) 当 $m$ 是
1
时,分数 $\frac{8}{m}$ 的倒数等于 8 的倒数。
答案:1
(2) 已知 $a$ 和 $b$ 互为倒数,则 $\frac{5}{a}$ 和 $\frac{6}{b}$ 的积是
30
。($a$、$b$ 不为 0)
答案:30
解析:
因为$a$和$b$互为倒数,所以$ab = 1$。
$\frac{5}{a} × \frac{6}{b} = \frac{5 × 6}{ab} = \frac{30}{ab}$
将$ab = 1$代入上式,得$\frac{30}{1} = 30$。
30
6. 新考法·数形结合 如图,直线上有 $a$、$b$、$c$、$d$ 四个数,其中有可能互为倒数的是(
B
)。

A.$a$ 和 $b$
B.$a$ 和 $c$
C.$b$ 和 $d$
D.$b$ 和 $c$
答案:B
解析:
由图可知:$0 < a < b < 1$,$c = 2$,$d = 3$。
互为倒数的两个数乘积为$1$。
A选项:$a$和$b$均小于$1$且大于$0$,则$a × b < 1$,不可能互为倒数。
B选项:$a$在$0$和$1$之间,$c = 2$,存在$a = \frac{1}{2}$时,$a × c = 1$,有可能互为倒数。
C选项:$b < 1$,$d = 3$,则$b × d < 3$且$b × d < 1 × 3 = 3$,但$b < 1$,所以$b × d < 3$且$b × d < 1 × 3 = 3$,实际$b × d < 1 × 3 = 3$,但$b < 1$,所以$b × d < 3$,又因为$b > 0$,所以$b × d > 0$,但$b < 1$,$d = 3$,则$b × d < 3$,且$b × d < 1 × 3 = 3$,不可能等于$1$(因为$b < 1$,$d = 3$,所以$b × d < 3$,且$b < 1$,所以$b × d < 1 × 3 = 3$,若$b × d = 1$,则$b = \frac{1}{3}$,但由图可知$b$接近$1$,但题目未明确$b$的具体值,不过从位置看$b$在$0$和$1$之间且靠近$1$,$\frac{1}{3}$相对更靠近$0$,所以可能性极小,且相比B选项,B选项更可能)。
D选项:$b < 1$,$c = 2$,则$b × c < 2$,但$b < 1$,所以$b × c < 2$,且$b > 0$,所以$b × c > 0$,但$b < 1$,$c = 2$,则$b × c < 2$,不可能等于$1$(因为$b < 1$,$c = 2$,所以$b × c < 2$,若$b × c = 1$,则$b = \frac{1}{2}$,但由图可知$a$和$b$均在$0$和$1$之间,且$a < b$,若$b = \frac{1}{2}$,则$a$更小,而$c = 2$,此时$a$可能更小,所以$b$不太可能是$\frac{1}{2}$,相比之下B选项$a$更可能是$\frac{1}{2}$)。
结论:选择B。
7. 已知 $a × \frac{9}{8} = b × \frac{8}{9} = c$($a$、$b$、$c$ 都大于 0),将 $a$、$b$、$c$ 三个数按从大到小的顺序排列。
答案:b>c>a
解析:
设$a×\frac{9}{8}=b×\frac{8}{9}=c=1$
则$a=1÷\frac{9}{8}=\frac{8}{9}$
$b=1÷\frac{8}{9}=\frac{9}{8}$
$c=1$
因为$\frac{9}{8}>1>\frac{8}{9}$,所以$b>c>a$
8. (易错题) 两个质数的倒数之和是 $\frac{12}{35}$,这两个质数分别是多少?
提示:倒数之和的分母是两个质数的积,分子是两个质数的和。
答案:把35分解质因数是35=5×7,而7+5=12,所以这两个质数分别是5和7。
解析:
因为两个质数的倒数之和的分母是这两个质数的积,分子是这两个质数的和。已知倒数之和是$\frac{12}{35}$,所以将$35$分解质因数:$35 = 5 × 7$,且$5 + 7 = 12$,故这两个质数分别是$5$和$7$。
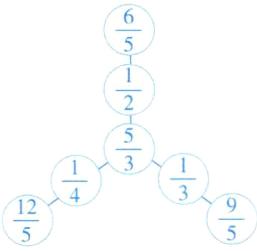
9. 把 $\frac{1}{2}$、$\frac{1}{3}$、$\frac{1}{4}$、$\frac{5}{3}$、$\frac{12}{5}$、$\frac{6}{5}$ 和 $\frac{9}{5}$ 这七个数填入下面的 $◯$ 里,使每条线上三个数的乘积都是 1。

答案: