1. 新考法·知识本质 学习了平行四边形的面积公式后,天天和同同想自己探究三角形的面积公式,他们发现两个
完全一样
的三角形可以拼成一个平行四边形(如图)。
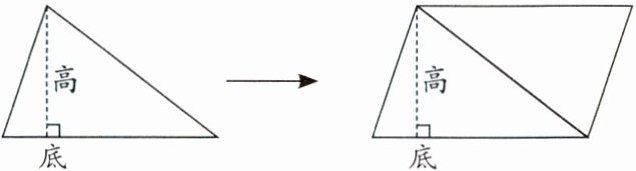
平行四边形的底相当于三角形的
底
,平行四边形的高相当于三角形的
高
,拼成的平行四边形的面积=
底
×
高
,所以三角形的面积=
底
×
高
÷2,如果用a和h分别表示三角形的底和高,那么三角形的面积S=
a× h÷ 2
。
答案:完全一样 底 高 底 高 底 高 $a× h÷ 2$
2. 荣德小学开展“跳蚤市场”活动日,为吸引小顾客,各班制作了各具特色的宣传标牌。下面是五年级制作的其中三张,你能分别求出它们的面积吗?(单位:dm)

答案:(1)$12× 18÷ 2=108$($\text{dm}^2$)
(2)$3× 4÷ 2=6$($\text{dm}^2$)
(3)$16× 15÷ 2=120$($\text{dm}^2$)
【点拨】利用公式计算三角形的面积时,要找准对应的底和高。
3. 如图,不能求出该三角形面积的算式是(
C
)。

A.$5a÷2$
B.$12h÷2$
C.$ah÷2$
答案:C
4. (易错题)荣德小学五(1)班有一块面积为$60m^{2}$的三角形实践基地(如图),这块实践基地的高是多少米?

答案:$60× 2÷ 15=8$(m)
答:这块实践基地的高是8m。
5. 绿地被称为城市之肺,在维护生态平衡、实现碳中和方面起到重要作用。为保护生态环境,城市建设公司对百花游园中的一块三角形绿地(如图)进行扩建。若将这块绿地的底延长4m,高扩大到原来的3倍,则一共扩建了多少平方米?

答案:$(15+4)× (12× 3)÷ 2=342$($\text{m}^2$)
$15× 12÷ 2=90$($\text{m}^2$)
$342-90=252$($\text{m}^2$)
答:一共扩建了$252\text{m}^2$。
【点拨】先根据已知条件求出扩建前、后三角形绿地的面积,再相减就是扩建的面积。
6. 利用旋转拼接,可以将复杂图形转化成简单图形,发现其中的数学技巧之美!如图,大三角形ABC分成了一个正方形和三角形甲、乙。甲、乙面积之和为39平方厘米,正方形的面积是多少平方厘米?

答案:$39× 2÷ (4+9)=6$(厘米)
$6× 6=36$(平方厘米)
答:正方形的面积是36平方厘米。
【点拨】根据题图可知三角形甲、乙都是直角三角形,且都有一条直角边等于正方形的边长。旋转三角形乙可以将三角形甲、乙拼接成一个底是(4+9)厘米,高等于正方形边长的三角形,已知三角形甲、乙面积之和,利用三角形的面积公式即可求出正方形的边长,再根据正方形的面积公式即可求出正方形的面积。