(1) 在下面方格纸中分别画一个面积是$8cm^{2}$的平行四边形、三角形和梯形。(每个小方格表示$1cm^{2}$)

答案:
(画法不唯一)
(2) 新情境·先贤智慧《蝶几谱》是中国古代组合家具的设计图。“几”是指桌型器具,“蝶几”的桌面有6种基本形状,共13张(如下图),可以根据需要自由拼组。

①《蝶几谱》中有一种拼组好的桌面,名为“葵实”,形状如下图。这张“葵实”桌面的面积是( )$dm^{2}$。
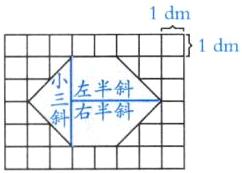
②“葵实”可以由哪几种基本形状的桌面拼组成?把你的拼组方案画在下图中。(注意每种基本形状桌面的张数)

答案:①16 ②如图,“葵实”可以由小三斜、左半斜、右半斜这三种基本形状的桌面拼组成。(答案不唯一)
(1) 公园里有一块平行四边形土地,在这块土地上已建成了平行四边形的牡丹园和三角形的杜鹃园(如下图),已知牡丹园的面积是$200m^{2}$。

①杜鹃园的面积是多少平方米?
②剩余土地的面积是多少平方米?
答案:①200÷20=10(m)
20×10÷2=100(m²)
答:杜鹃园的面积是100m²。
[点拨]先根据“平行四边形的高=面积÷底”求出牡丹园的高,根据题意可知杜鹃园的高与牡丹园的高相等,已知杜鹃园的底,即可求出杜鹃园的面积。
②(20+20+20)×10-200-100=300(m²)
答:剩余土地的面积是300m²。
[点拨]根据题意可知这块平行四边形土地的高与牡丹园的高相等,先根据图中数据求出这块平行四边形土地的底,再根据面积公式求出这块平行四边形土地的面积,最后减去牡丹园、杜鹃园的面积,就是剩余土地的面积。
(2) 在校园环境中,花坛不仅美化了校园环境,还为学生提供了一个亲近自然、感受生命美好的场所。典典的学校有一座梯形小花坛,种植了一些月季(如图中涂色部分),中间修了两条观赏路(如图中空白部分)。种花部分的面积有多大?如果种植月季每平方米需要85元,一共需要多少元?

答案:(9-2-2+15-2-2)×6÷2=48(m²)
48×85=4080(元)
答:种花部分的面积是48m²,一共需要4080元。
[点拨]通过平移可以将种花部分的面积转化成上底是(9-2-2)m,下底是(15-2-2)m,高是6m的梯形的面积。
(3) 学校准备将一块上底为6米的梯形空地改建成学生活动场地,如果这个梯形的上底延长3米,面积就增加12平方米,且原来的梯形变成了平行四边形,则原来这块梯形空地的面积是多少平方米?
答案:12×2÷3=8(米)
(6+6+3)×8÷2=60(平方米)
答:原来这块梯形空地的面积是60平方米。
[点拨]根据题意可知,梯形的上底延长3米,这个梯形就多出一个与它等高的三角形,三角形的底是3米,面积是12平方米,根据“三角形的高=面积×2÷底”求出三角形的高,即梯形的高。上底延长3米后,梯形变成了平行四边形,所以梯形的下底比上底长3米,根据梯形的面积公式即可求出原来这块梯形空地的面积。