(1) 一个梯形的上底是5厘米,下底是7厘米,高是8厘米。如果上底增加3厘米,下底减少3厘米,那么变化后的梯形的面积是(
48
)平方厘米。
答案:(1)48【点拨】上底增加3厘米,下底减少3厘米,则上、下底之和为上底+3厘米+下底-3厘米=上底+下底,因此变化前后的上、下底之和不变,上底+下底=5+7=12(厘米),根据梯形的面积公式可求出变化后的梯形的面积是12×8÷2=48(平方厘米)。
解析:
变化后的上底为$5 + 3 = 8$厘米,下底为$7 - 3 = 4$厘米。上、下底之和为$8 + 4 = 12$厘米。梯形面积公式为$S = \frac{(a + b)h}{2}$,其中$a$、$b$为上、下底,$h$为高。代入得$S = \frac{12×8}{2} = 48$平方厘米。
48
(2) 一个梯形的上、下底之和是15米,面积是120平方米,这个梯形的高是(
16
)米。
答案:(2)16【点拨】根据梯形的面积=(上底+下底)×高÷2可知,高=面积×2÷(上底+下底),代入数据求得梯形的高是120×2÷15=16(米)。
解析:
根据梯形面积公式:$S = \frac{(a + b)h}{2}$(其中$S$表示面积,$a + b$表示上、下底之和,$h$表示高),可得$h = \frac{2S}{a + b}$。
已知$a + b = 15$米,$S = 120$平方米,代入公式得:
$h = \frac{2×120}{15} = \frac{240}{15} = 16$(米)
16
(3) 一幅直角梯形拼图,上底2分米,下底6分米,两腰分别长3分米和5分米,这幅直角梯形拼图的面积是(
12
)平方分米。
答案:(3)12【点拨】直角梯形较短的一条腰也是梯形的高,因此这个直角梯形的高是3分米,然后根据梯形的面积公式可求出梯形的面积是(2+6)×3÷2=12(平方分米)。
解析:
直角梯形较短的腰为高,即高是3分米。
面积为$(2 + 6) × 3 ÷ 2 = 12$平方分米。
12
2. 典典学习了梯形的面积后,分别在长方形和平行四边形中绘制出两个不同的梯形(如图),你能求出它们各自的面积吗?(单位:cm)
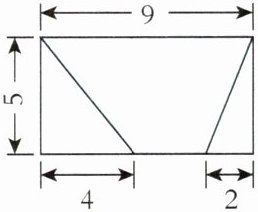

答案:(9-4-2+9)×5÷2=30(cm²)(16-9+16)×12÷2=138(cm²)
3. 发展灌溉排水,调节地区水情是保障农业增产的措施之一。明华村修建了一条灌溉渠(如图),横截面是梯形,渠口宽12米,渠底宽4米,面积为48平方米。则这条灌溉渠深多少米?

答案:48×2÷(4+12)=6(米)答:这条灌溉渠深6米。【点拨】根据“梯形的高=面积×2÷(上底+下底)”列式计算。
解析:
48×2÷(12+4)=6(米)
答:这条灌溉渠深6米。
4. 手工折纸是同学们最喜欢的手工操作。龙龙用一张长方形纸片折成了一个梯形(如图,单位:厘米),这个梯形的面积是多少平方厘米?

答案:(12+12+6+6)×8÷2=144(平方厘米)答:这个梯形的面积是144平方厘米。
5. (易错题)在下图中,梯形的下底是17 cm,高是5 cm,两个底角都是45°,求梯形的面积。

答案:(17-5×2+17)×5÷2=60(cm²)答:梯形的面积是60cm²。【点拨】因为等腰直角三角形的两条直角边相等,所以题图中梯形的下底比上底长(5×2)cm,先根据下底求出上底,再根据梯形的面积公式求出梯形的面积。
解析:
上底:$17 - 5×2 = 7\,\text{cm}$
面积:$\frac{(7 + 17)×5}{2} = 60\,\text{cm}^2$
答:梯形的面积是$60\,\text{cm}^2$。
6. 如图,梯形ABCD被它的一条对角线BD分成了两部分。三角形BDC的面积比三角形ABD的面积大10平方分米。已知梯形的下底与上底的长度之和是15分米,长度之差是5分米,则梯形ABCD的面积是多少平方分米?

答案:10×2÷5=4(分米)15×4÷2=30(平方分米)答:梯形ABCD的面积是30平方分米。【点拨】三角形BDC、三角形ABD各有一条和梯形ABCD长度相等的高,这条高对应的三角形BDC的底是BC,三角形ABD的底是AD。根据“三角形BDC的面积比三角形ABD的面积大10平方分米”可知这条高是10×2÷5=4(分米)。再根据“梯形的面积=(上底+下底)×高÷2”列式即可求出梯形ABCD的面积。
解析:
设梯形的上底为$AD$,下底为$BC$,梯形的高为$h$。
因为三角形$ABD$和三角形$BDC$的高都等于梯形的高$h$,所以$S_{\triangle BDC}-S_{\triangle ABD}=\frac{1}{2}BC\cdot h - \frac{1}{2}AD\cdot h=\frac{1}{2}(BC - AD)h$。
已知$BC - AD = 5$分米,$S_{\triangle BDC}-S_{\triangle ABD}=10$平方分米,可得$\frac{1}{2}×5× h = 10$,解得$h=\frac{10×2}{5}=4$分米。
又因为$AD + BC = 15$分米,所以梯形$ABCD$的面积为$\frac{1}{2}(AD + BC)\cdot h=\frac{1}{2}×15×4 = 30$平方分米。
答:梯形$ABCD$的面积是$30$平方分米。