9. (2025·吉林长春期中)已知$|a|= 2,|b|= 1$,且$a<b$,求$a+b$的值.
答案:
∵|a|=2,|b|=1,
∴a=±2,b=±1.
∵a<b,
∴a=-2,b=1或a=-2,b=-1,
当a=-2,b=1时,a + b=-2 + 1=-1;
当a=-2,b=-1时,a + b=-2+(-1)=-3.
综上,a + b的值为-1或-3.
归纳总结本题考查了有理数的加法、绝对值,确定a,b 的值是解题的关键.
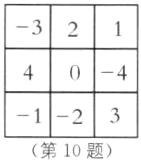
10. 将$-4,-3,-2,-1,0,1,2,3,4$这九个数分别填入下面的方阵,使横、竖及斜对角的三个数相加的和都相等.

答案:答案不唯一.如图所示:
11. (1)比较大小(用“<”“>”或“=”填空).
①$|+2|+|-3|$
>
$|(+2)+(-3)|$;
②$|-2|+|-3|$
=
$|(-2)+(-3)|$;
③$|0|+|-3|$
=
$|0+(-3)|$.
(2)在(1)的基础上,小淇又举出若干个例子,并归纳得出以下结论,请你补充完整:
①当$a,b$
异号
(填“同号”或“异号”)时有$|a|+|b|>|a+b|$;
②当$a,b$
同号
(填“同号”或“异号”)时有$|a|+|b|= |a+b|$;
③当$a,b$中至少有一个为0时,有$|a|+|b|$
=
$|a+b|$.
(3)根据上述结论,请你直接写出当$|x|+2024= |x-2024|$时,$x$的取值范围.
∵|x|+2024=|x-2024|.
∴|x|+|-2024|=|x+(-2024)|.
由(2)可知,x=0或x与-2024同号
故x的取值范围是x≤0.
答案:
(1)①> ②= ③=
(2)①异号 ②同号 ③=
(3)
∵|x|+2024=|x-2024|.
∴|x|+|-2024|=|x+(-2024)|.
由
(2)可知,x=0或x与-2024同号
故x的取值范围是x≤0.
关键提醒 本题考查有理数的加法和有理数的绝对值,解题关键是掌握相关概念和法则.
12. (2024·陕西中考)小华探究“幻方”时,提出了一个问题:如图,将$0,-2,-1,1,2$这五个数分别填在五个小正方形内,使横向三个数之和与纵向三个数之和相等,则填入中间位置的小正方形内的数可以是______(答案不唯一).(写出一个符合题意的数即可)

答案:0(答案不唯一) [解析]解法一:由题意,填写如图
(1):

1+0+(-1)=0,2+0+(-2)=0,满足题意.
解法二:由题意,填写如图
(2):
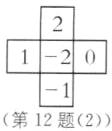
1+(-2)+0=-1,2+(-2)+(-1)=-1,满足题意.
解法三:由题意,填写如图
(3):

(-1)+2+0=1,(-2)+2+1=1,满足题意.
方法技巧 本题考查了有理数的运算,根据横向三个数之和与纵向三个数之和相等,进行填写即可得出结果.