1. (2024·广东中考)计算$-5+3$的结果是(
A
).
A.$-2$
B.$-8$
C.$2$
D.$8$
答案:A
解析:
$-5+3=-(5-3)=-2$,结果为$-2$,对应选项A。
2. 若$x的相反数是2$,$|y|= 5$,则$x+y$的值为(
D
).
A.$-7$
B.$7或3$
C.$7或-3$
D.$3或-7$
答案:D
解析:
因为$x$的相反数是$2$,所以$x=-2$。
因为$|y| = 5$,所以$y = 5$或$y=-5$。
当$x=-2$,$y = 5$时,$x + y=-2+5=3$;
当$x=-2$,$y=-5$时,$x + y=-2+(-5)=-7$。
故$x + y$的值为$3$或$-7$。
D
3. 比$-4\frac{2}{3}大而比2$小的所有整数的和为
-9
.
答案:-9
解析:
比$-4\frac{2}{3}$大而比$2$小的整数有$-4$,$-3$,$-2$,$-1$,$0$,$1$。
它们的和为:$-4 + (-3) + (-2) + (-1) + 0 + 1$
$=(-4 - 3 - 2 - 1) + (0 + 1)$
$=-10 + 1$
$=-9$
$-9$
4. (教材P34例1·变式)计算:
(1)$(+2)+(+6)$;
(2)$(-2)+(-6)$;
(3)$(+2)+(-6)$;
(4)$(-2)+(+6)$.
答案:
(1)8
(2)-8
(3)-4
(4)4
5. 对于有理数$a,b$,有下列几种说法,其中正确的说法个数是(
A
).
①若$a+b= 0$,则$a与b$互为相反数;
②若$a+b<0$,则$a与b$异号;
③若$a+b>0$,则$a与b$同号,则$a>0,b>0$;
④若$|a|>|b|$,且$a,b$异号,则$a+b>0$;
⑤若$|a|<b$,则$a+b>0$.
A.$3$
B.$2$
C.$1$
D.$0$
答案:A [解析]①若a + b = 0,则a = - b,即a与b互为相反数,故①正确;
②若a = - 1,b = - 2,则a + b = - 3<0,但是a与b同号,故②错误;
③若a + b>0,且a与b同号,则a,b同时为正,故a>0,b>0,故③正确;
④若a = - 3,b = 2,满足条件|a|>|b|,且a,b异号,但是a + b = - 1<0,故④错误;
⑤若|a|<b,则b>0,a + b>0,故⑤正确.则正确的结论有3个.
故选A
6. 新情境 设计“幻方” 爱动脑筋的小明同学设计了如图所示的“幻方”游戏图,将$1,-2,3,-4,5,-6,7,-8$分别填入图中的圆圈内,使得横、竖以及内外两个正方形的4个数字之和都相等,他已经将$-4,5,7,-8$这四个数填入了圆圈,则图中$a+b$的值为______.
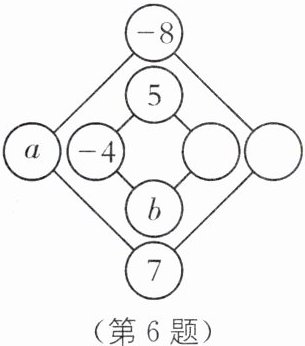
-5或-8
答案:-5或-8 [解析]
∵这8个数字的和是 - 4,
∴横、竖以及内外两个正方形的4个数字之和都等于 - 2,根据题意有 - 8 + 5 + b + 7 = - 2,解得b = - 6.
根据内圈正方形的4个数字之和等于 - 2,得内圈右边的圆圈应填3,则a = 1或 - 2,
因此a + b = - 5或 - 8.
7. 传统文化 “正负术” (2025·南通如皋期末)我国是历史上最早认识和使用负数的国家.数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.根据刘徽的这种表示法,图(1)表示算式$(+1)+(-1)= 0$,则图(2)表示的算式为
(+2)+(-4)=-2
.
答案:(+2)+(-4)=-2
8. 方程思想 (2025·浙江金华期中)如图,串联在一起的每个曲别针下方挂着一张写有整数的卡片,从左到右,第1个至第3个曲别针所挂卡片上的整数分别为$-3,-5,2$.
(1)求前三个曲别针所挂卡片上数的和;
(2)若后两个数绝对值的和比前两个数的和的绝对值大3,请求出第4个数.
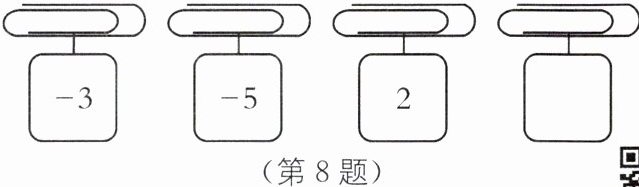
答案:
(1)(-3)+(-5)+2=-6.
(2)|(-3)+(-5)|=8,8 + 3 = 11,设第4个数为x,则|2|+|x|=11,即|x|=9,
∴x=±9,
∴第四个数为±9.
思路引导 本题考查有理数的加法和绝对值,掌握相关知识点是解题的关键