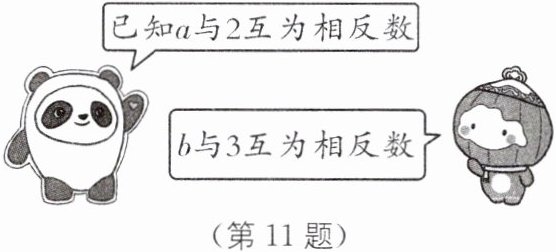
11. (2025·甘肃兰州华侨教育集团期中改编)请根据图示的对话解答下列问题.
(1)$a = $
-2
,$b = $
-3
.
(2)已知$|m - a| + |b + n| = 0$,求 m,n 的值.
$\because |m-a|+|b+n|=0$,
$\therefore m-a=0,b+n=0$,
又$a=-2,b=-3$,
$\therefore m=-2,n=3$.
答案:
(1)-2 -3 [解析]$\because a$与2互为相反数,而2的相反数是-2,
$\therefore a=-2$.
$\because b$与3互为相反数,而-3的相反数是3,
$\therefore b=-3$.
(2)$\because |m-a|+|b+n|=0$,
$\therefore m-a=0,b+n=0$,
又$a=-2,b=-3$,
$\therefore m=-2,n=3$.
12. 分类讨论思想 已知点 A 在数轴上对应的数为 a,点 B 在数轴上对应的数为 b,且$|a + 4| + |b - 1| = 0$,A,B 之间的距离记作$|AB|$.
(1)求 A,B 之间的距离$|AB|$;
(2)设点 P 在数轴上对应的数为 x,当$|PA| - |PB| = 2$时,求 x 的值.
精题详解
答案:(1)因为$|a+4|+|b-1|=0$,
所以$a+4=0,b-1=0$,
所以$a=-4,b=1$,所以$|AB|=5$.
(2)$|PA|-|PB|=2$,即点P到点A的距离比点P到点B的距离大2个单位长度.
画数轴如下:

若点P在点A的左侧,则点P到点B的距离大于点P到点A的距离,不符合题意;
若点P在点A和点B之间,由题知$|AB|=5,5-2=3,3÷2=1.5$,则点P与点A的距离为3.5个单位长度,与点B的距离为1.5个单位长度时,符合题意,此时$x=-0.5$;
若点P在点B右侧,$|PA|-|PB|=5$,不符合题意.
13. 中考新考法 新定义问题 对于数轴上的两点 P,Q 给出如下定义:P,Q 两点到原点 O 的距离之差的绝对值称为 P,Q 两点的绝对距离,记为$|POQ|$.
例如:P,Q 两点表示的数,所示,则$|POQ| = |PO - QO| = |3 - 1| = 2$. A,B 两点表示的数如图(2)所示:

(1)求 A,B 两点的绝对距离;
(2)若 C 为数轴上一点(不与点 O 重合),且$|AOB| = 2|AOC|$,求点 C 表示的数.
精题详解
答案:
(1)$|AOB|=|OA-OB|=|1-3|=2$,
即A,B两点的绝对距离为2.
(2)因为$|AOB|=2,|AOB|=2|AOC|$,
所以$|AOC|=1$.
又点A所表示的数是1,即$OA=1$,
所以$|AOC|=|OA-OC|=1$,即$|1-OC|=1$,
所以$OC=0$或$OC=2$.
又点C不与点O重合,所以$OC=2$.
所以点C表示的数为-2或2.