1. (2025·盐城建湖期中)某市对市区主干道进行绿化,现有甲、乙两个施工队,甲施工队有13位工人,乙施工队有27位工人,现计划有变,需要从乙施工队借调x名工人到甲施工队,刚好甲施工队人数是乙施工队人数的3倍,则根据题意列出方程正确的是(
B
).
A.3(13+x)= 27-x
B.13+x= 3(27-x)
C.3(13-x)= 27+x
D.13-x= 3(27+x)
答案:B
解析:
从乙施工队借调$x$名工人到甲施工队后,甲施工队人数为$13 + x$,乙施工队人数为$27 - x$。
因为此时甲施工队人数是乙施工队人数的3倍,所以可列方程:$13 + x = 3(27 - x)$。
B
2. (2025·南京玄武区期末)已知x= 2是关于x的方程$\frac{5}{2}x-2a= 0$的解,则代数式2a-1的值是(
B
).
A.3
B.4
C.5
D.6
答案:B
解析:
将$x = 2$代入方程$\frac{5}{2}x - 2a = 0$,得$\frac{5}{2} × 2 - 2a = 0$,即$5 - 2a = 0$,解得$2a = 5$,则$2a - 1 = 5 - 1 = 4$。
B
3. 课本习题中有一个方程$\frac{x-■}{2}= x+3,$其中一个数字被污渍盖住了,书后该方程的答案为x= -7,那么■处的数字应是(
C
).
A.-5
B.-1
C.1
D.5
答案:解析 设■表示的数为a,
∵x=-7是方程$\frac{x-a}{2}=x+3$的解,
∴$\frac{-7-a}{2}=-7+3,$解得a=1,即■=1.故选C.
4. 如果用“a= b”表示一个等式,c表示一个整式,d表示一个数,那么等式的第一条性质就可以表示为“a±c= b±c”,以下借助符号正确地表示出等式的第二条性质的是(
D
).
A.a·c= b·d,a÷c= b÷d
B.a·d= b÷d,a÷d= b·d
C.a·d= b·d,a÷d= b÷d
D.a·d= b·d,a÷d= b÷d(d≠0)
答案:D
5. (2025·宿迁沭阳县期末)小琪同学在某月的月历上圈出了三个数a,b,c,并求出了它们的和为30,则这三个数在月历中的排列位置不可能是(
D
).
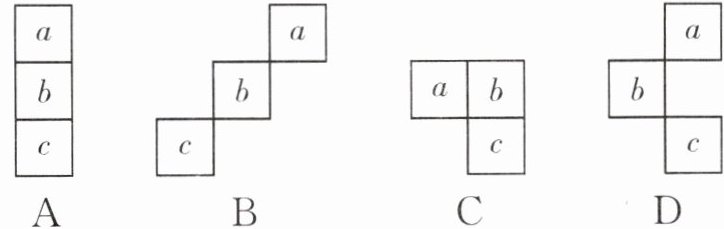
A.
B.
C.
D.
答案:解析 A.根据题意,得a+b+c=30,
∴b-7+b+b+7=30,解得b=10,选项A不符合题意;B.根据题意,得a+b+c=30,
∴b-6+b+b+6=30,解得b=10,选项B不符合题意;C.根据题意,得a+b+c=30,
∴b-1+b+b+7=30,解得b=8,选项C不符合题意;D.根据题意,得a+b+c=30,
∴b-6+b+b+8=30,解得$b=\frac{28}{3},$选项D符合题意.故选D.
6. 已知关于x的方程2x+a-5= 0的解是x= 2,则a的值为(
B
).
A.3
B.1
C.2
D.-1
答案:解析 将x=2代入2x+a-5=0,
∴2×2+a-5=0,
∴a=1.故选B.
7. 数形结合思想 已知一个小长方形的长和宽分别是x和2,当5个形状、大小相同的小长方形拼成一个如图所示的大长方形,所标尺寸如图所示,图中阴影部分面积是(
C
).
A.18
B.27
C.29
D.33
答案:解析 由题图,得(x+2×2)(x+2)=2x×5+S_{阴影},
∵5=x+2-2×2,
∴x=7,
∴S_{阴影}=11×9-2×7×5=29.故选C.
8. (2025·宿迁泗洪一模)我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清,醑酒各几何?”大意为:现有一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿30斗谷子,共换了5斗酒,问清酒,醑酒各几斗? 如果设清酒x斗,那么可列方程为(
A
$).A. 10x+3(5-x)= 30 B. 3x+10(5-x)= 30C. \frac{x}{3}+\frac{30-x}{10}= 5 D. \frac{x}{10}+\frac{30-x}{3}= 5$
答案:A
解析:
设清酒为$x$斗,则醑酒为$(5 - x)$斗。因为一斗清酒价值10斗谷子,所以$x$斗清酒价值$10x$斗谷子;一斗醑酒价值3斗谷子,所以$(5 - x)$斗醑酒价值$3(5 - x)$斗谷子。已知共拿30斗谷子换酒,可列方程:$10x + 3(5 - x) = 30$。
A
9. 已知方程(a+3)x^{|a|-2}+2= a-3是关于x的一元一次方程,则a= ______
3
.
答案:解析
∵方程(a+3)x^{|a|-2}+2=a-3是关于x的一元一次方程,
∴|a|-2=1,a+3≠0,解得a=3.
10. 如果代数式6x-5与5x+16互为相反数,那么x=
-1
.
答案:解析 根据题意,得6x-5+5x+16=0,移项,得6x+5x=5-16,合并同类项,得11x=-11,系数化为1,得x=-1.
11. 传统文化 《算法统宗》 (2025·苏州相城区期末)明代数学家程大位的《算法统宗》中有这样一个问题:“隔墙听得客分银,不知人数不知银,七两分之多四两,九两分之少半斤.”其大意为:有一群人分银子,若每人分七两,则剩余四两,若每人分九两,则还差半斤(注:明代时1斤= 16两,故有“半斤八两”这个成语).设有x人分银子,根据题意列方程:
7x+4=9x-8
.
答案:7x+4=9x-8