【例】某同学晚上6点多钟开始做作业,他家墙上时钟的时针和分针的夹角是120°,他做完作业后还是当天晚上6点多钟,且时针和分针的夹角还是120°,此同学做作业大约用了(
C
).
A.40分钟
B.42分钟
C.44分钟
D.46分钟
解析:设开始做作业时的时间是6点x分,∴6x-0.5x= 180-120,解得x≈11;再设做完作业后的时间是6点y分,∴6y-0.5y= 180+120,解得y≈55,∴此同学做作业大约用了55-11= 44(分钟).
答案:C
答案:【解析】:
本题考查的是钟面上的夹角问题。
需要知道时针和分针每分钟转动的角度。
分针每分钟转动$6 ^{\circ}$(因为分针每小时转动360度,即每分钟转动$\frac{360 ^{\circ}}{60} = 6 ^{\circ}$)。
时针每小时转动$30 ^{\circ}$(因为时针12小时转360度,即每小时转动$\frac{360 ^{\circ}}{12} = 30 ^{\circ}$),所以时针每分钟转动$\frac{30 ^{\circ}}{60} = 0.5 ^{\circ}$。
由于时针在上,分针在下,
所以需要考虑到时针和分针的相对角度。
设开始做作业的时间是6点x分,此时时针和分针的夹角为$120 ^{\circ}$。
分针转动的角度为$6x$,时针转动的角度为$0.5x$,
由于6点整时,时针和分针的夹角为$180 ^{\circ}$,
所以在6点x分时,时针和分针的相对角度为$6x - 0.5x = 180 ^{\circ} - 120 ^{\circ}$。
解这个方程,得到$x \approx 11$。
设做完作业的时间是6点y分,此时时针和分针的夹角仍然为$120 ^{\circ}$。
同样地,可以列出方程$6y - 0.5y = 180 ^{\circ} + 120 ^{\circ}$(注意这里是加$120 ^{\circ}$,因为此时分针已经超过了时针,所以夹角是分针和时针之间的角度加上一个$120 ^{\circ}$的基础夹角)。
解这个方程,得到$y \approx 55$。
因此,做作业所用的时间大约是$y - x = 55 - 11 = 44 (分钟)$。
【答案】:
C
1.(全国初中数学联赛江西南昌竞赛试卷)直线a上有四个不同的点,依次为点A,B,C,D,则到点A,B,C,D的距离之和最小的点(
D
).
A.可以是直线AD外的某一点
B.只是点B和点C
C.只是线段AD的中点
D.有无数多个
答案:D
解析:
设直线$a$上四个点$A,B,C,D$的坐标分别为$a,b,c,d$,且$a < b < c < d$,点$P$坐标为$x$。距离之和$S=|x - a| + |x - b| + |x - c| + |x - d|$。
当$x < a$时,$S=(a - x)+(b - x)+(c - x)+(d - x)=(a + b + c + d)-4x$,随$x$增大而减小;
当$a \leq x < b$时,$S=(x - a)+(b - x)+(c - x)+(d - x)=(b + c + d - a)-2x$,随$x$增大而减小;
当$b \leq x \leq c$时,$S=(x - a)+(x - b)+(c - x)+(d - x)=(c + d - a - b)$,为定值;
当$c < x \leq d$时,$S=(x - a)+(x - b)+(x - c)+(d - x)=(2x)+(d - a - b - c)$,随$x$增大而增大;
当$x > d$时,$S=(x - a)+(x - b)+(x - c)+(x - d)=4x-(a + b + c + d)$,随$x$增大而增大。
综上,当点$P$在线段$BC$上(含端点$B,C$)时,距离之和最小,故这样的点有无数多个。
D
2.(第二十届“希望杯”全国数学邀请赛第一试)在数轴上,表示整数的点称为“整点”.设数轴的单位长度是1 cm,若在这条数轴上随意画出一条长为2008 cm的线段AB,则线段AB盖住的整点至少有(
C
).
A.2006个
B.2007个
C.2008个
D.2009个
答案:C
解析:
当线段AB的起点在整点时,终点也在整点,盖住的整点个数为2008+1=2009个;当线段AB的起点不在整点时,起点在两个整点之间,终点也在两个整点之间,盖住的整点个数为2008个。所以线段AB盖住的整点至少有2008个。
C
3.已知n(n≥2)个点$P_1,P_2,P_3,…,Pₙ$在同一平面内,且其中没有任何三点在同一直线上.设Sₙ表示过这n个点中的任意2个点所作的所有直线的条数,显然$,S_2= 1,S_3= 3,S_4= 6,S_5= 10,…,$由此推断,Sₙ= __
$\frac{n(n - 1)}{2}$
_.
答案:$\frac{n(n - 1)}{2}$ [解析]
∵$S_{2}=1=\frac{2×1}{2}$,
$S_{3}=3=1 + 2=\frac{2×3}{2}$,$S_{4}=6=1 + 2 + 3=\frac{3×4}{2}$,
∴$S_{n}=1 + 2 + 3 + \cdots + (n - 1)=\frac{n(n - 1)}{2}$。
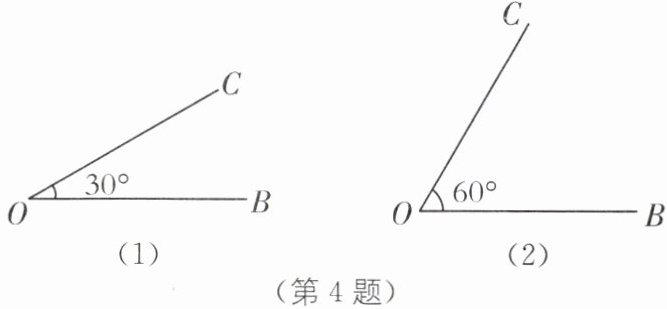
4.给出如下定义:如果∠AOC+∠BOC= 90°,且∠AOC= k∠BOC(k为正整数),那么称∠AOC是∠BOC的“倍锐角”.
(1)已知∠AOC+∠BOC= 90°,下列三个条件中,能判断∠AOC是∠BOC的“倍锐角”的是___(填写序号);
①∠BOC= 15°;②∠AOC= 70°;③OC是∠AOB的平分线.
(2)如图(1),当∠BOC= 30°时,在图中画出∠BOC的一个“倍锐角”∠AOC;
(3)如图(2),当∠BOC= 60°时,射线OB绕点O旋转,每次旋转10°,可得它的“倍锐角”∠AOC= ___;
(4)当∠BOC= m°且存在它的“倍锐角”∠AOC时,则∠AOB= ___.
答案:4.
(1)①③ [解析]①由∠BOC = 15°,∠AOC + ∠BOC = 90°,得∠AOC = 75° = 5∠BOC,
∴∠AOC是∠BOC的“倍锐角”;
②由∠AOC = 70°,∠AOC + ∠BOC = 90°,得∠BOC = 20°,两个角不是整数倍关系,
∴∠AOC不是∠BOC的“倍锐角”;
③
∵OC平分∠AOB,∠AOC + ∠BOC = 90°,
∴∠AOC = ∠BOC = 45°,
∴∠AOC是∠BOC的“倍锐角”;
综上所述,能判断∠AOC是∠BOC的“倍锐角”的是①③。
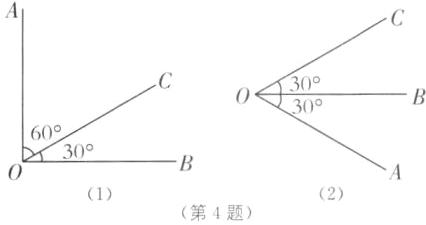
(2)由∠BOC = 30°,∠AOC + ∠BOC = 90°,
得∠AOC = 60° = 2∠BOC。
有两种情况,如图
(1)和图
(2)所示:
(3)80°或60° [解析]
∵∠BOC = 60°,且射线OB绕点O每次旋转10°,
∴∠BOC的取值有0°,10°,20°,30°,40°,50°,60°,70°,80°,90°这几种,对每个可能的值进行分析可知,只有两种情况下,∠AOC是∠BOC的“倍锐角”:
①当∠BOC = 10°时,∠AOC = 80° = 8∠BOC;
②当∠BOC = 30°时,∠AOC = 60° = 2∠BOC,
∴∠AOC = 80°或60°。
(4)90°或(90 - 2m)° [解析]若∠BOC存在它的“倍锐角”∠AOC时,其几何图示有图
(3)和图
(4)中画出的两种情况:

①如图
(3),当OA在OC的上方时,
∠AOB = ∠AOC + ∠BOC = 90°;
②如图
(4),当OA在OC的下方时,
∠AOB = ∠AOC - ∠BOC = 90° - ∠BOC - ∠BOC = (90 - 2m)°,
∴∠AOB = 90°或(90 - 2m)°。