1. 如图,过点 O 任意画一条直线,把平行四边形分成了两个图形,下列说法正确的是(
C
)。
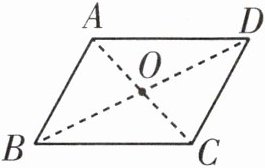
A.两个图形形状不同,面积相等
B.两个图形形状相同,面积不等
C.两个图形形状相同,面积相等
D.两个图形形状不同,面积不等
答案:1.C
2. 如图,长方形 ABCF 与长方形 ACDE 部分重叠。三角形①的面积是 8 平方厘米,三角形②的面积是(
B
)平方厘米。

A.12
B.16
C.24
D.40
答案:2.B
解析:
长方形ABCF面积:$8×6 = 48$平方厘米,三角形ABC面积:$\frac{1}{2}×8×6=24$平方厘米,三角形AFC面积 = 长方形ABCF面积 - 三角形ABC面积 = $48 - 24=24$平方厘米。
长方形ACDE面积 = 三角形AFC面积 + 三角形①面积 = $24 + 8=32$平方厘米,AC长度 = 长方形ABCF的对角线,由勾股定理得$AC=\sqrt{8^{2}+6^{2}} = 10$厘米,长方形ACDE的宽AE = 长方形ACDE面积÷AC = $32÷10 = 3.2$厘米,长方形ACDE的长AD = 长方形ACDE面积÷AE = $32÷3.2 = 10$厘米(AC=AD=10厘米,符合长方形邻边关系)。
三角形ACD面积:$\frac{1}{2}×10×3.2 = 16$平方厘米,三角形②面积 = 三角形ACD面积 = 16平方厘米。
B
3. 如图,每个平行四边形的底都是 20 厘米,高都是 12 厘米。它们中涂色部分的面积是 120 平方厘米的共有
C
个。

A.1
B.2
C.3
D.4
答案:3.C
解析:
每个平行四边形面积:$20×12 = 240$平方厘米。
图1:涂色三角形底20厘米,高12厘米,面积$\frac{1}{2}×20×12 = 120$平方厘米。
图2:涂色部分为三个三角形,底之和20厘米,高12厘米,面积$\frac{1}{2}×20×12 = 120$平方厘米。
图3:涂色部分为两个三角形,底之和20厘米,高12厘米,面积$\frac{1}{2}×20×12 = 120$平方厘米。
图4:涂色三角形底20厘米,高12厘米,面积$\frac{1}{2}×20×12 = 120$平方厘米。
共有4个。
C
4. 如图,在给定的正方形方格顶点上(每个小方格表示 1 平方厘米)找一点 C,使点 C 和线段 AB 围成的三角形的面积是 2 平方厘米,符合条件的点 C 共有(
D
)个。

A.5
B.6
C.8
D.10
答案:4.D
解析:
由图可知,AB长为2厘米,设点C到AB的距离为h厘米。三角形面积公式为$S = \frac{1}{2} × 底 × 高$,则$\frac{1}{2} × 2 × h = 2$,解得$h = 2$。
AB在水平方向,距离AB为2厘米的直线有两条(AB上方2厘米和下方2厘米)。
AB上方2厘米的直线上,方格顶点有5个;AB下方2厘米的直线上,方格顶点有5个。
符合条件的点C共有$5 + 5 = 10$个。
D
5. 如图,已知正方形 ABCD 的边长为 10 厘米,四边形 EFGH 的面积是 9 平方厘米,则涂色部分的面积是(
B
)平方厘米。

A.28
B.32
C.41
D.42
答案:5.B
解析:
连接AC,设AF与BE交于点E,AF与BG交于点F,CH与DG交于点G,CH与DE交于点H。
正方形ABCD面积:$10×10=100$平方厘米。
$\triangle ABC$和$\triangle ADC$面积均为:$\frac{1}{2}×10×10=50$平方厘米。
设空白部分面积为$S$,涂色部分面积为$S_{涂}$,则$S + S_{涂}=100$。
空白部分由四个三角形组成,其面积和为$2×(50 - S_{涂} - 9)$,即$S=2×(50 - S_{涂} - 9)$。
联立得:$2×(50 - S_{涂} - 9)+S_{涂}=100$,解得$S_{涂}=32$。
32
四、计算题
计算下图中涂色部分的面积。(单位:厘米)


答案:6×10÷2=30(平方厘米)
18×12÷2=108(平方厘米)
10×10÷2=50(平方厘米)
8×8 - 5×5=39(平方厘米)
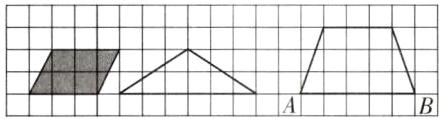
1. 下面方格图中每个小方格表示 1 平方厘米。
(1) 画一个与已知平行四边形面积相等、高也相等的三角形。
(2) 以 AB 为下底,画一个面积是 12 平方厘米的梯形。

答案:1.
(1)
(2)如图,画法不唯一。
2. 如图,求图中涂色部分①②的面积和。
方法一:将图①向右平移,与图②拼成一个长方形,求面积和。
列式计算:
2.4×8=32(平方厘米)
。
方法二:将图①和图②分别割补转化成梯形,求面积和。
列式计算:
(6+2)×4÷2×2=32(平方厘米)
。
答案:2.4×8=32(平方厘米)
(6+2)×4÷2×2=32(平方厘米)
5. 如图,在长方形 ABCD 中,AB = 24 厘米,AD = 16 厘米。一个动点 P 从顶点 A 出发,逆时针沿长方形的边以每秒 2 厘米的速度运动回到点 A。
(1) 点 P 从点 A 出发最少经过多少秒时,三角形 ABP 的面积最大?
8
(2) 三角形 ABP 最大面积共持续(
12
)秒。
答案:5.
(1)16÷2=8(秒)
(2)12 提示:
(1)当点P运动到线段DC上时,三角形ABP的面积最大。从点A出发逆时针走,求最少时间即求到达点D的时间,已知AD为16厘米,运动速度为每秒2厘米,所以需要16÷2=8(秒)到达点D。
(2)当点P在线段DC上时,三角形ABP面积最大,所以持续24÷2=12(秒)。