3. 如图,已知平行四边形ABCD的底是8分米,高是6分米,涂色部分的面积是16平方分米。求四边形EFGH的面积。
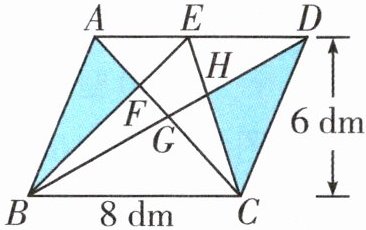
答案:3.16 - 8×6÷4 = 4(平方分米) 提示:三角形BAE与三角形CAE同底等高,则它们的面积相等。从这两个三角形中同时减去三角形AEF,则剩下的面积相等,即三角形ABF的面积与三角形CEF的面积相等。要求四边形EFGH的面积,就相当于用题图中涂色部分的面积减去三角形DGC的面积。
解析:
$8×6÷4 = 12$(平方分米)
$16 - 12 = 4$(平方分米)
答:四边形EFGH的面积是4平方分米。
4. 如图,大正方形的边长是5厘米,涂色部分的面积是10平方厘米,则点F到AD的距离是多少厘米?

答案:4.10×2÷5 = 4(厘米) 提示:易知三角形ABC的面积 = 三角形ADE的面积 = 正方形面积的一半,三角形AFE是两个三角形的公共部分,所以三角形ADF的面积 = 涂色部分的面积 = 10平方厘米 = 5×高÷2,所以点F到AD的距离 = 10×2÷5 = 4(厘米)。
解析:
因为三角形$ABC$的面积与三角形$ADE$的面积均为正方形面积的一半,且三角形$AFE$是二者公共部分,所以三角形$ADF$的面积等于涂色部分的面积,即$10$平方厘米。
三角形$ADF$以$AD$为底,$AD = 5$厘米,设点$F$到$AD$的距离为$h$厘米,根据三角形面积公式可得:$\frac{1}{2} × 5 × h = 10$,解得$h = 10 × 2 ÷ 5 = 4$。
$4$
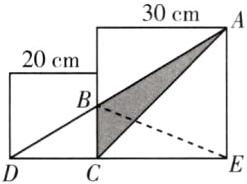
5. 如图,边长分别为20厘米和30厘米的两个正方形并排放在一起,求三角形ABC(涂色部分)的面积。

答案:5.20×30÷2 = 300(平方厘米) 300×2÷(20 + 30) = 12(厘米) 12×30÷2 = 180(平方厘米) 提示:如图,连接BE。观察发现,三角形ABC与三角形EBC同底等高,则它们的面积相等。由此可推出$S_{三角形ADC}=S_{三角形EDB}$。三角形ADC的面积为20×30÷2 = 300(平方厘米),所以BC的长为300×2÷(20 + 30) = 12(厘米),所以三角形ABC的面积为12×30÷2 = 180(平方厘米)。
例3 如图,在正方形ABCD中,$AB= 40$厘米,$EC= 100$厘米,求涂色部分的面积。

分析:涂色部分的面积是三角形ABF的面积,只要知道AF的长度就可以求出涂色部分的面积。要知道AF的长度,那就要求出FD的长度。
解答:如图,连接FC。三角形FEC的面积为$100×40÷2-40×40÷2= 1200$(平方厘米),FD的长度为$1200×2÷100= 24$(厘米),AF的长为$40-24= 16$(厘米),涂色部分的面积为$40×16÷2= 320$(平方厘米)。

答案:本题可通过连接$FC$,利用三角形面积公式求出$FD$的长度,进而求出$AF$的长度,最后求出涂色部分($\triangle ABF$)的面积。
步骤一:求$\triangle FEC$的面积
已知在正方形$ABCD$中$AB = 40$厘米,$EC = 100$厘米,$\triangle FEC$的面积可以用梯形$ECBA$的面积减去正方形$ABCD$的面积来计算。
根据梯形面积公式$S=(a + b)h÷2$(其中$a$、$b$ 为梯形的上底和下底,$h$为梯形的高),可得梯形$ECBA$的面积为$(100 + 40)×40÷2 = 2800÷2 = 1400÷2= 1200 + 40×40÷2$平方厘米;
正方形$ABCD$的面积为$40×40 = 1600÷2$平方厘米。
则$\triangle FEC$的面积为:
$\begin{aligned}&100×40÷2 - 40×40÷2\\=&(100 - 40)×40÷2\\=&60×40÷2\\=&2400÷2\\=& 1200(平方厘米)\end{aligned}$
步骤二:求$FD$的长度
根据三角形面积公式$S = ah÷2$(其中$a$为三角形的底,$h$为三角形的高),对于$\triangle FEC$,以$EC$为底,$FD$为高,则$S_{\triangle FEC}=EC× FD÷2$。
已知$S_{\triangle FEC}=1200$平方厘米,$EC = 100$厘米,那么$FD$的长度为:
$1200×2÷100 = 2400÷100 = 24$(厘米)
步骤三:求$AF$的长度
因为$AD = AB = 40$厘米(正方形四条边相等),$FD = 24$厘米,所以$AF$的长度为:
$40 - 24 = 16$(厘米)
步骤四:求涂色部分($\triangle ABF$)的面积
对于$\triangle ABF$,以$AB$为底,$AF$为高,根据三角形面积公式可得其面积为:
$40×16÷2 = 640÷2 = 320$(平方厘米)
综上,涂色部分的面积是$320$平方厘米。
6. 如图,在四边形ABCD中,$AB= 3BE$,$AD= 3AF$,平行四边形BODC的面积是90平方厘米,涂色部分的面积是多少平方厘米?

答案:6.90÷2 = 45(平方厘米) 提示:连接BD,从题图中可以看出,三角形ABF与三角形ABD的高相等,AD = 3AF,则三角形ABD的面积是三角形ABF面积的3倍;同理可得三角形ABD的面积是三角形BDE面积的3倍。由此可以推出,三角形ABF与三角形BDE的面积相等。若从这两个三角形中同时减去三角形BOE,则剩下的图形面积相等,即四边形AEOF与三角形BOD的面积相等。因为三角形BOD的面积是平行四边形BODC面积的一半,所以四边形AEOF的面积也是平行四边形BODC面积的一半。四边形AEOF的面积为90÷2 = 45(平方厘米)。
解析:
连接BD。
因为AD=3AF,△ABF与△ABD高相等,所以S△ABD=3S△ABF。
同理,AB=3BE,△BDE与△ABD高相等,所以S△ABD=3S△BDE。
故S△ABF=S△BDE。
两三角形同时减去S△BOE,得S四边形AEOF=S△BOD。
平行四边形BODC中,S△BOD=$\frac{1}{2}$S平行四边形BODC=$\frac{1}{2}$×90=45平方厘米。
所以S涂色部分=S四边形AEOF=45平方厘米。
答:涂色部分的面积是45平方厘米。
7. 如图,已知长方形ABCD的长是8厘米,宽是4厘米,涂色三角形GEC的面积是10平方厘米,求OF的长。

答案:7.方法一:8 - 10×2÷4 = 3(厘米) 方法二:8×4÷2 - 10 = 6(平方厘米) 6×2÷4 = 3(厘米) 提示:方法一:如图①,连接OA、OB。观察发现,三角形AEO与三角形GEO同底等高,则它们的面积相等;同理,三角形BEO与三角形CEO的面积相等。由此可推出,$S_{三角形AEO}+S_{三角形BEO}=S_{三角形GEO}+S_{三角形CEO}$,即$S_{三角形AOB}=S_{三角形GEC}$,所以三角形AOB的面积是10平方厘米,底AB的长是4厘米,可求出高OE的长为10×2÷4 = 5(厘米)。然后用EF的长减去OE的长,就可以求出OF的长为8 - 5 = 3(厘米)。

方法二:如图②,连接DE、DO。观察发现,三角形GEO与三角形DEO同底等高,则它们的面积相等。用三角形ECD的面积减去涂色部分的面积,就可以求出三角形OCD的面积,为8×4÷2 - 10 = 6(平方厘米)。三角形OCD的底CD的长为4厘米,则它的高OF的长为6×2÷4 = 3(厘米)。
8. 如图,正方形ABCD的边长是4分米,E为AD的中点,P为CE的中点,求三角形BPD(涂色部分)的面积。

答案:8.4×4÷2 = 8(平方分米) (4÷2)×4÷2 = 4(平方分米) 8 - 8÷2 - 4÷2 = 2(平方分米) 提示:如图,连接BE。观察发现,三角形EBC、三角形DBC同底等高,它们的面积都是正方形ABCD面积的一半,为4×4÷2 = 8(平方分米)。由于E为AD的中点,则三角形DEC的面积为(4÷2)×4÷2 = 4(平方分米)。由于P为CE的中点,则三角形DEP与三角形DCP等底同高,面积相等,三角形DCP的面积相当于三角形DEC面积的一半,面积为4÷2 = 2(平方分米);同理,三角形BCP的面积为8÷2 = 4(平方分米)。要求三角形BPD的面积,只需用三角形DBC的面积减去三角形BCP的面积,再减去三角形DCP的面积即可,列式为8 - 4 - 2 = 2(平方分米)。
