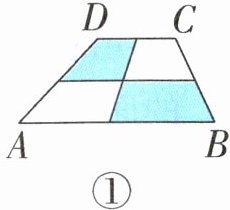
11. 应用意识 王明带了一把锄头和足够长的细线,想把一块梯形土地平均分成两部分,如图,王明利用对折细线的方法,找到四条边的中点,并按照如图①所示的方法将土地分成了面积相等的两部分,你能否再帮助王明设计两种不同的方案也将这块土地分成面积相等的两部分呢?

答案:答案合理即可,示例:设梯形上、下底分别为a、b,高为h。
方案一:如图①,连接梯形上、下底的中点G、F,则四边形AFGD的面积=四边形FBCG的面积=(a+b)×h÷4;
方案二:如图②,连接BD,取BD的中点E,连接AE、EC,则图中的四边形AECD的面积=梯形ABCD面积的一半。
因为DE=BE,所以三角形ABE的面积=三角形ADE的面积,三角形CBE的面积=三角形CDE的面积,三角形ABE的面积+三角形CBE的面积=三角形ADE的面积+三角形CDE的面积,所以四边形ABCE的面积=四边形AECD的面积=梯形ABCD面积的一半。
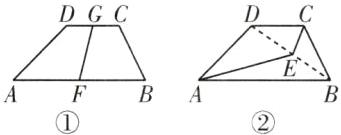
提示:第一种方法:利用两底的中点,将图形分割成两个梯形,它们的上、下底分别相等,高也相等,所以面积也相等。第二种方法:连接对角线BD,利用BD的中点E,连接CE和AE,则三角形ABE的面积=三角形ADE的面积,三角形CBE的面积=三角形CDE的面积,所以四边形AECD和四边形ABCE的面积相等。
12. 推理意识 老师让同学们计算AB.C + D.E时,马小虎把D.E中的小数点看漏了,得到错误结果39.6;而马大虎把加号看成了乘号,得到错误结果36.9,求正确的计算结果。
列竖式分析:

那么C = (
6
),E = (
5
),A + D = 3,所以B = 9 - E = (
4
)。
根据分析得AB.C + D.E = (
24.6
)+(
1.5
) = (
26.1
)。
答案:6 5 4 24.6 1.5 26.1
提示:根据四则运算中数与数计算的一些特征来推算。
13. 模型意识 【动手做】如图①,在纸上画平行四边形ABCD,连接对角线AC、BD,它们的交点O被称为平行四边形的中心。

过平行四边形的中心O任意画一条直线,把平行四边形分成了两个什么图形?这两个图形完全一样吗?先画一画,再把分成的两个图形剪下来比一比。
【拓展应用】如图③,过正方形的中心O画两条线段,可以将正方形分成4个完全一样的等腰直角三角形。

(1) 在图④和图⑤中,过中心O画两条线段,将正方形分成4个完全一样的图形。(用不同的方法画一画)
(2) 在图③中,AC和BD的长度都是20厘米,这个正方形的面积是( )平方厘米。
答案:如图,分成了两个完全一样的梯形、两个完全一样的三角形或两个完全一样的平行四边形。

(答案不唯一)
提示:尝试自己画图可知。
(1)如图:

(答案不唯一)
提示:过中心O画两条线段,用不同的方法将正方形分成4个完全一样的图形即可。
(2)200
提示:先根据条件计算出一个等腰直角三角形的面积,再乘4即可。20÷2=10(厘米),10×10÷2×4=200(平方厘米)。
14. 几何直观 雪花让人着迷,让我们来探究雪花的周长吧!
我们从简单情形入手,从一个边长是2.43毫米的等边三角形(如图)开始。
① 把等边三角形的各边三等分,从每条边三等分后的中段,向外作小等边三角形,再去掉与原等边三角形重叠的边;(为方便叙述,后面把这个过程简称为“变化”)
② 对上一步得到的小等边三角形,重复上面的“变化”;
③ 再对上一步得到的小等边三角形,重复上面的“变化”。

问题:第三步得到的雪花的周长是(
17.28
)毫米。
答案:17.28
提示:因为等边三角形的边长是2.43毫米,所以它的周长是2.43×3=7.29(毫米),认真观察题图,找出图形的变化规律和周长之间的关系,解答即可。第一步的周长为7.29+7.29÷3=9.72(毫米);第二步的周长为9.72+9.72÷3=12.96(毫米);第三步的周长为12.96+12.96÷3=17.28(毫米)。