6. 数形结合 如图,竖式计算的是整个大长方形的面积,竖式中“1584”表示(
B
)的面积和,一共是15.84平方分米。
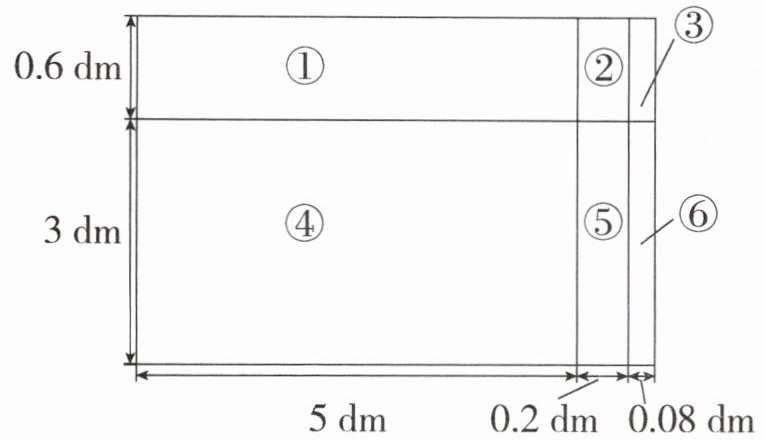

A.①②③
B.④⑤⑥
C.①④
D.③⑥
答案:B
提示:在竖式中,“1584”是“528×3”的结果,在题图中,④⑤⑥三部分组成的长方形的长是5.28分米,5.28分米在竖式计算时暂不看小数点就是“528”,3分米是④⑤⑥三部分组成的长方形的宽,所以“1584”表示的是④⑤⑥的面积和。
7. 正难则反 如图,甲、乙面积相差多少?

答案:34×16−34×30÷2=34(平方厘米)
提示:甲的面积和乙的面积无法直接求出,观察题图可以发现,甲+空白梯形=平行四边形,乙+空白梯形=大三角形,则甲的面积−乙的面积=平行四边形的面积−大三角形的面积=34×16−34×30÷2=34(平方厘米)。
8. 量不变思想 如图,直角梯形ABCD中,AB = 8厘米,BC = 6厘米,CD = 4厘米,两涂色部分面积相差18平方厘米,ED的长是多少厘米?

答案:(4+8)×6÷2=36(平方厘米) (36−18)×2÷6=6(厘米) 6−4=2(厘米)
提示:涂色部分面积之差即为梯形ABCD和三角形BCE面积之差,先求出梯形面积,再求出三角形面积,进而可求出CE的长,最后可求出DE的长。
9. 间接法 如图①所示,梯形的上底AB = 5厘米,下底CD = 9厘米,DE = 3厘米,EC = 6厘米,高是4厘米,涂色部分的面积是多少?数学课上,同学们的方法很多,下面是三位同学的解题方法。
小华的方法:梯形ABCD的面积 - 三角形ABE的面积 = (5 + 9)×4÷2 - 5×4÷2 = 18(平方厘米)
小明的方法:三角形ADE的面积 + 三角形BEC的面积 = 3×4÷2 + 6×4÷2 = 18(平方厘米)
小红的方法:4×9÷2 = 18(平方厘米)

(1) 请你用算式、文字等方法说明小红的方法是对的。
(2) 如图②,梯形的上底是5厘米,下底是8厘米,高是5厘米,求涂色部分的面积。
答案:
(1)因为涂色部分面积等于两个三角形面积之和,又因为三角形的面积=底×高÷2,所以4×6÷2+4×3÷2=4×(6+3)÷2=4×9÷2=18(平方厘米),所以小红的方法是对的。
(2)8×5÷2=20(平方厘米)
提示:
(1)涂色部分的两个三角形的底的和是3 + 6 = 9(厘米),等于梯形的下底9厘米,高都是4厘米,因此这两个三角形的面积之和可以看作底是(3 + 6)厘米,高是4厘米的三角形的面积。
(2)涂色部分的三个三角形的底的和就等于梯形的下底8厘米,高都是5厘米,所以涂色部分的面积就是底是8厘米,高是5厘米的三角形的面积。
10. 知识迁移 在电脑编程世界里,可以用数组来存放数,数组是什么呢?请先阅读,并完成相关习题:
(1) 比如数组A(2),它有A(0)、A(1)、A(2)3个变量,那么就可以存放3个数;数组B(10)有B(0) ~ B(10)11个变量,那么可以存放11个数。
① 数组A(100)可以存放(
101
)个数。
② 要想数组A正好存放240个数,数组可表示为(
A(239)
)。
(2) 刚才介绍的是一维数组,那么二维数组A(1,2)有A(0,0)、A(0,1)、A(0,2)、A(1,0)、A(1,1)、A(1,2)6个变量,可以存放6个数;二维数组A(4,7)有5×8 = 40(个)变量,可以存放40个数。
① 数组E(49,8)可以存放(
450
)个数。
② 要想数组A正好存放323个数,用二维数组可表示为(
A(16,18)
)。
答案:
(1)①101 ②A
(239)
提示:①通过观察可以发现,数组A(n)可以存放(n+1)个数,所以A
(100)可以存放100+1=101(个)数。②要想正好存放240个数,则n=240−1=239,数组可以表示为A
(239)。
(2)①450 ②A(16,18)(答案不唯一)
提示:①通过观察二维数组可以发现,数组内的两个数分别加上1,然后再相乘,就可以得到存放的数的个数。则数组E(49,8)可以存放(49+1)×(8+1)=450(个)数。②要想正好存放323个数,需要先把323写成两个数相乘的形式,再把这两个数分别减去1。例如:323=17×19,所以数组内的两个数分别是17−1=16,19−1=18。