9. 扬州市召开出租车运价改革方案听证会,其中某方案为不超过3千米为起步价,超过3千米的部分按每千米另收费(不足1千米的按1千米计)。小王说:“我乘出租车走了5千米,付了12.8元。”小张说:“我乘出租车走了9千米,付了22.4元。”请你算一算,这种方案出租车的起步价是多少元?超过3千米后,每千米的车费是多少元?
答案:超过3千米后,每千米的车费:(22.4−12.8)÷(9−5)=2.4(元) 起步价:12.8−2.4×(5−3)=8(元) 或22.4−2.4×(9−3)=8(元)
解析:
超过3千米后,每千米的车费:$(22.4 - 12.8) ÷ (9 - 5) = 2.4\ \text{元}$
起步价:$12.8 - 2.4 × (5 - 3) = 8\ \text{元}$
|与墙垂直的边/米|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
|与墙平行的边/米|
14
|
12
|
10
|
8
|
6
|
4
|
2
|
|面积/平方米|
14
|
24
|
30
|
32
|
30
|
24
|
14
|
有
7
种不同的围法,面积最大是
32
平方米。
答案:与墙垂直的边/米 1 2 3 4 5 6 7
与墙平行的边/米 14 12 10 8 6 4 2
面积/平方米 14 24 30 32 30 24 14
7种 面积最大是32平方米
11. 许达从家去少年宫,只能向西或向南走,一共有多少种不同的走法?如果许达还要经过泛书房买书,一共有多少种不同的走法?
]
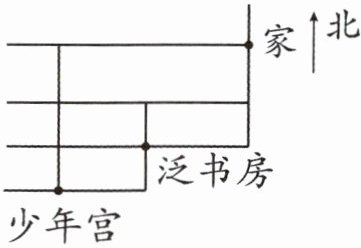
答案:6种 4种 提示:如图:

12. 用一架天平和1克、3克、9克的砝码各一个,你知道能称出多少种不同质量的物体吗?(左盘除了物体也能放砝码)
]

答案:13种 提示:从选取的砝码的个数想起。只选1个砝码,有3种称法,能称出的物体的质量分别为1克、3克和9克。选2个砝码,放在天平的一边,有3种称法,能称出的物体的质量分别为1+3=4(克),1+9=10(克),3+9=12(克);放在天平的两边,也有3种称法,能称出的物体的质量分别为3−1=2(克),9−1=8(克),9−3=6(克)。选3个砝码,放在天平的一边,只有1种称法,能称出的物体的质量是1+3+9=13(克);放在天平的两边,有3种称法,能称出的物体的质量分别为9−1−3=5(克),9+1−3=7(克),9+3−1=11(克)。可见,能称出1克至13克不同质量的物体。
解析:
1个砝码:1克,3克,9克,共3种;
2个砝码(同边):1+3=4克,1+9=10克,3+9=12克,共3种;
2个砝码(两边):3-1=2克,9-1=8克,9-3=6克,共3种;
3个砝码(同边):1+3+9=13克,共1种;
3个砝码(两边):9-1-3=5克,9+1-3=7克,9+3-1=11克,共3种;
综上,能称出1克至13克共13种不同质量的物体。
13种
13. 婷婷要演出12天,她请裁缝店的王师傅做演出服,要求每天穿的服装搭配不相同。如果做一件衬衣80元,做一条裙子或裤子50元。婷婷的演出服至少需要多少元?
答案:80×3+50×4=440(元)
所以婷婷的演出服至少需要$440$元。
14. 小林做了3只骰子,每只骰子的6个面上分别写着2个“1”、2个“2”和2个“3”。每次同时抛起3只骰子,落下后,朝上的3个数字可能会出现多少种不同的情况?(不考虑顺序)
]

答案:1. 三个数字都相同:(1,1,1)、(2,2,2)、(3,3,3),共3种。
2. 两个数字相同,一个不同:(1,1,2)、(1,1,3)、(2,2,1)、(2,2,3)、(3,3,1)、(3,3,2),共6种。
3. 三个数字都不同:(1,2,3),共1种。
3+6+1=10
答:朝上的3个数字可能会出现10种不同的情况。