7. 小明的父亲喜欢打台球,小明经常观看,他发现当球撞向桌边的时候就会向另一个方向弹走,如(1)中图。
(1)请量出下面每个角的度数。
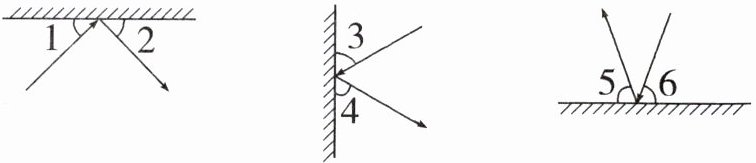
$∠1= $( ) $∠3= $( ) $∠5= $( )
$∠2= $( ) $∠4= $( ) $∠6= $( )
我发现：______。
(2)运用发现的规律,补充下面台球的运动路线图。
答案：(1)∠1=40°，∠3=30°，∠5=50°，∠2=40°，∠4=30°，∠6=50°。我发现：台球撞向桌边时，入射角等于反射角。
(2)
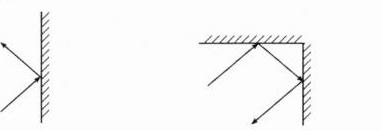
1. 已知$∠1= 40^{\circ }$,$∠5$是直角,分别求出$∠2$、$∠3$、$∠4$的度数。
答案：∠2=90°−40°=50° ∠3=180°−50°=130°∠4=180°−130°=50°
2. 如图,$∠2的度数比∠1$的4倍多$5^{\circ }$,$∠2$是多少度？
答案：∠1=(180°−5°)÷(4+1)=35° ∠2=180°−35°=145°
3. 点O在长方形的正中间(如图),如果点O到直线a的距离是5厘米,到直线c的距离是7厘米,这个长方形的周长是多少厘米？面积是多少平方厘米？
答案：周长:(7×2+5×2)×2=48(厘米)面积:(7×2)×(5×2)=140(平方厘米)
解析：
长方形的长为$7×2 = 14$厘米，宽为$5×2 = 10$厘米。
周长：$(14 + 10)×2 = 48$厘米
面积：$14×10 = 140$平方厘米
4. 如图,已知$∠1+∠2+∠3= 220^{\circ }$,求$∠3$的度数。
答案：∠1=220°−180°=40° ∠3=180°−40°=140°
答案：
(1)15 提示:5+4+3+2+1=15(个)。
(2)18 提示:基本长方形有6个，由2个基本长方形组成的长方形有7个，由3个基本长方形组成的长方形有2个，由4个基本长方形组成的长方形有2个，由6个基本长方形组成的长方形有1个，一共有6+7+2+2+1=18(个)长方形。
强基直通车 如图,$∠2+∠3= ∠1+∠4$,当$∠AOB= $(
36
)°时,图中所有锐角的和是$180^{\circ }$。
答案：36 提示:题图中共有10个锐角,分别是∠1、∠2、∠3、∠4、∠1+∠2、∠2+∠3、∠3+∠4、∠1+∠2+∠3、∠2+∠3+∠4、∠1+∠2+∠3+∠4。10个锐角的和为4(∠1+∠4)+6(∠2+∠3)=180°。因为∠2+∠3=∠1+∠4,所以10(∠1+∠4)=180°,即∠1+∠4=18°,所以∠AOB=∠1+∠4+∠2+∠3=2(∠1+∠4)=36°。
解析：
图中共有10个锐角，分别是∠1、∠2、∠3、∠4、∠1+∠2、∠2+∠3、∠3+∠4、∠1+∠2+∠3、∠2+∠3+∠4、∠1+∠2+∠3+∠4。
10个锐角的和为∠1+∠2+∠3+∠4+(∠1+∠2)+(∠2+∠3)+(∠3+∠4)+(∠1+∠2+∠3)+(∠2+∠3+∠4)+(∠1+∠2+∠3+∠4)=4(∠1+∠4)+6(∠2+∠3)。
已知所有锐角和为180°，则4(∠1+∠4)+6(∠2+∠3)=180°。
因为∠2+∠3=∠1+∠4，设∠1+∠4=∠2+∠3=x，所以4x+6x=180°，10x=180°，解得x=18°。
∠AOB=∠1+∠2+∠3+∠4=(∠1+∠4)+(∠2+∠3)=x+x=2x=2×18°=36°。
36
