例1 如图,一辆汽车在一条笔直的公路AB上由点A向点B行驶,点M、N分别是位于公路AB同一侧的两个村庄。
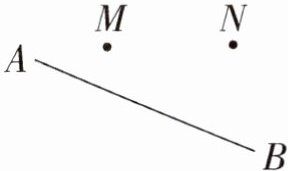
设汽车行驶到公路AB上点O的位置时,到两个村庄的距离之和最小。请在图中画出点O的位置。
分析:根据两点之间线段最短的知识,运用转化思想,可以帮助我们有效地确定点O的位置。
两点之间线段最短,已知M、N两个村庄在公路的同一侧。可以假设把村庄M搬到公路的另一侧,过点M向AB画一条垂线,在垂线上找到点M',使点M'到直线AB的距离与点M到直线AB的距离相等,此时点M'为点M关于直线AB的对称点。连接M'N,与直线AB相交于一点,此点即为O。除了找点M的对称点,也可以找点N的对称点。确定点O位置的画法不唯一。
答案:
1. 李叔叔从家(点A)出发到河边挑水,然后再到田里(点B)浇水,怎样走路线最短?画一画。

答案:如图所示。(画法不唯一)

提示:要使路线最短,就是使点A与挑水的点、挑水的点与点B的连线的长度之和最小。我们可以以河为对称轴,作点A的对称点A₁,连接A₁B,交河岸于点C,则点C就是我们要找的挑水点。AC的长度=A₁C的长度。(轴对称图形折叠后重合的点是对应点,叫作对称点)
2. (1)李老师从湖中的小岛O处开始划船,先用最短时间到AB岸,再用最短时间到CD岸,最后返回小岛O,请在图①中画出最短路线。
(2)李老师从湖中的小岛O处开始划船,先到AB岸,再到CD岸,最后返回小岛O,请在图②中画出最短路线。

答案:(1)

提示:根据垂直线段最短,先从O处向直线AB作垂直线段OM,再从点M向直线CD作垂直线段MN,最后连接NO,“OM→MN→NO”即为整个过程的最短路线。
(2)

提示:首先画出点O关于直线AB的对称点G,同理,画出点O关于直线CD的对称点H,连接GH,交AB于点M,交CD于点N,从而可得GM=OM,NH=NO,所以GH=GM+MN+NH=OM+MN+NO。因为两点之间线段最短,所以线段GH最短,即线段OM、MN、NO的长度之和最小,则OM→MN→NO即为最短路线。
例2 如图,图中共有多少个三角形?

分析:要数图中的三角形的个数,可以先数以DE上的线段为边的三角形的个数,有1+2+3= 6(个)。再数以BC上的线段为边的三角形的个数,也有1+2+3= 6(个),所以图中共有6+6= 12(个)三角形。
答案:解析:本题考查了三角形的计数方法,通过分别计算不同底边对应的三角形个数,再求和得到总数。
答案:
以$DE$为底边,从左到右三角形个数依次为:$1 + 2 + 3 = 6$(个);
以$BC$为底边,从左到右三角形个数依次为:$1 + 2 + 3 = 6$(个);
则图中三角形总数为:$6 + 6 = 12$(个)。
答:图中共有$12$个三角形。