1. (1)1个周角= (
4
)个直角
1个周角= (
2
)个平角
(2)写出下面各角的名称,并把它们按度数的大小从小到大排列(写序号)。
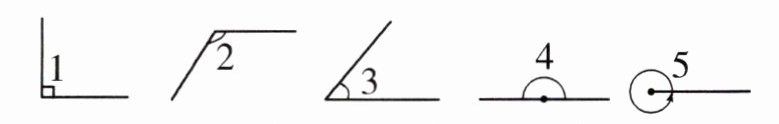
(
直
)角 (
钝
)角 (
锐
)角 (
平
)角 (
周
)角
(
∠3
)<(
∠1
)<(
∠2
)<(
∠4
)<(
∠5
)
(3)亚冬会上有一位单板滑雪运动员做了一个动作是“空中翻转$1080^{\circ }$”,是指该运动员空中翻转(
3
)圈。
(4)5时整,钟面上时针与分针所夹的较小角是(
150
)$^{\circ }$。从5时到6时,时针转过(
30
)$^{\circ }$,形成的角是(
锐
)角;分针转过(
360
)$^{\circ }$,形成的角是(
周
)角。
答案:1.
(1)4 2
(2)直 钝 锐 平 周 ∠3 ∠1 ∠2 ∠4 ∠5
(3)3
(4)150 30 锐 360 周
2. 画一画。
(1)以图①射线作为角的一条边,用量角器画出$80^{\circ }$的角。
(2)以图②中的点A为顶点,画一个比直角大$15^{\circ }$的角。

答案:2.
(1)

(2)

(画法不唯一,合理即可)
3. 下面由一副三角尺拼成的角分别是多少度?是什么角?

75
度,是
锐
角;
120
度,是
钝
角;
15
度,是
锐
角。
答案:3.75 锐 120 钝 15 锐
(1)两个锐角不可能拼成一个
C
。
A.钝角
B.直角
C.平角
答案:C
(2)一个锐角,可以用三角尺上的一个角量两次得到,这个锐角是( )。
A.$30^{\circ }$
B.$45^{\circ }$
C.$60^{\circ }$
答案:C
(3)钟面上秒针旋转一周,那么分针旋转的角度是( );分针转动$360^{\circ }$,相应地,时针转动( )。
A.$1^{\circ }$
B.$6^{\circ }$
C.$10^{\circ }$
D.$30^{\circ }$
答案:B D
5. (1)小明在《角的分类》这一篇数学日记中,将角的度数在直线上表示出来。图上$∠A$是(
锐
)角,$∠B$是(
直
)角,$∠C$是(
钝
)角,$∠D$是(
平
)角,$∠E$是(
周
)角。
(2)

(
3
)个钝角
(
3
)个直角
(
8
)个锐角
(3)分针指向12,若时针和分针成$60^{\circ }$角,则钟面上的时间是(
2
)时或(
10
)时。
答案:5.
(1)锐 直 钝 平 周
(2)3 3 8
(3)2 110