6. (1)用一副三角尺画$150^{\circ }和15^{\circ }$的角。(保留画图痕迹)
(2)还有哪些度数的角是可以用一副三角尺画出来的?再列举3个。______ ______ ______
答案:6.
(1)如图(画法不唯一)。


(2)105° 75° 120°(答案不唯一)
7. (1)将一副直角三角尺如图①摆放,比一比:$∠1◯ ∠3$。
=
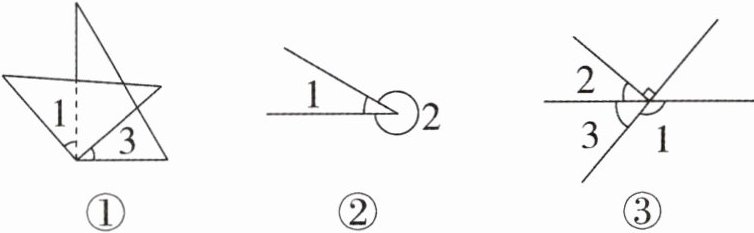
(2)如图②,$∠1= 30^{\circ }$,$∠2= ( )^{\circ }$。
330
(3)如图③,$∠1= 130^{\circ }$,$∠2= ( )^{\circ }$。
40
(4)如图是一张长方形纸折起来后的图形。

$∠2= 120^{\circ }$
$∠1= ( )^{\circ }$
30
$∠3= ( )^{\circ }$
90
(5)如图,$∠2是∠1$的8倍。

$∠1= ( )^{\circ }$
20
$∠2= ( )^{\circ }$
160
答案:7.
(1)=
(2)330
(3)40
(4)30 90
(5)20 160
8. 整体思想 如图,将一张长方形纸的一角折过去,使角的顶点A落在点$A'$处,BC为折痕,再将它的

另一个角也斜折过去,并使BD边与$BD'$重合,折痕为BE。
(1)已知$∠ABC= 55^{\circ }$,那么$∠2= $
35
°,$∠CBE= $
90
°。
(2)如果改变$∠ABC$的大小,则$BD'$的位置也随之改变,那么$∠CBE$的大小会不会改变?请说明理由。
无论∠ABC的度数怎样变化,∠CBE的度数都是∠1、∠2的度数和,都是∠ABD度数的一半,即90°,所以∠CBE的大小不会改变。
答案:8.
(1)35 90
提示:∠1、∠2是折叠所形成的角,所以∠1=∠ABC=55°,∠2=(180°−55°×2)÷2=35°。∠CBE=∠1+∠2=55°+35°=90°。
(2)无论∠ABC的度数怎样变化,∠CBE的度数都是∠1、∠2的度数和,都是∠ABD度数的一半,即90°,所以∠CBE的大小不会改变。
提示:∠1与∠ABC,∠2与∠DBE,这4个角组成一个平角,∠CBE的大小始终是平角的一半,即180°÷2=90°。
9. (1)

$∠1+∠2= 140^{\circ }$
$∠2+∠3= 120^{\circ }$
$∠2= $
80
°
(2)

$∠1+∠2+∠3= 180^{\circ }$
$∠4+∠5+∠6= $
360°
答案:9.
(1)80
提示:方法一:∠2=(∠1+∠2)+(∠2+∠3)−(∠1+∠2+∠3)=140°+120°−180°=80°。
方法二:∠3=180°−(∠1+∠2)=40°,∠2=120°−∠3=80°。
(2)360°
提示:∠1与∠4,∠2与∠6,∠3与∠5都拼成了一个平角,即180°,且∠1+∠2+∠3=180°,所以∠4+∠5+∠6=180°×3−180°=360°。
10. 如图,O是直线AD上一点,$∠BOC比∠AOB大30^{\circ }$,$∠COD比∠BOC大30^{\circ }$,则$∠AOB$是(
30
)$^{\circ }$。

答案:10.30
提示:方法一:∠BOC比∠AOB大30°,∠COD比∠BOC大30°,那么∠COD比∠AOB大两个30°,∠AOB+∠BOC+∠COD=180°,所以用180°减去∠BOC比∠AOB多的部分及∠COD比∠AOB多的部分,即为3倍的∠AOB。
方法二:∠AOB=∠BOC−30°,∠COD=∠BOC+30°,且∠COD+∠BOC+∠AOB=180°,即(∠BOC+30°)+∠BOC+(∠BOC−30°)=180°,所以∠BOC=60°,所以∠AOB=60°−30°=30°。
11. 有序思想 如图,$∠1= ∠2= ∠3$,图中所有锐角的度数和是$200^{\circ }$,$∠1$是多少度?

答案:11.∠1=200°÷(3+2+2+3)=20°
提示:题图中有6个锐角,分别是∠1、∠2、∠3、∠1+∠2、∠2+∠3、∠1+∠2+∠3,共10个∠1。