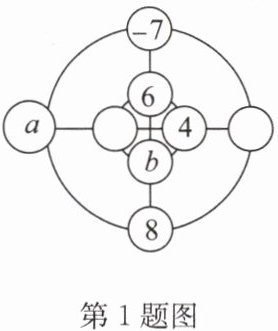
1. 大家喜欢玩的幻方游戏,老师稍加创新改成了“幻圆”游戏,现在将$-1,2,-3,4,-5,$$6,-7,8$分别填入图中的圆圈内,使横、竖以及内外两圈上的4个数字之和都相等,老师已经帮助同学们完成了部分填空,则图中$a+b$的值为 ( )
A.$-6或-3$
B.$-8$或1
C.$-1或-4$
D.1或$-1$
答案:A 点拨:如答图,设小圈上的数为c,大圈上的数为d,−1+2−3+4−5+6−7+8=4.因为横、竖以及内外两圈上的4个数字之和都相等,所以两个圈上的数字和是2,横、竖上的数字和也各是2,所以−7+6+b+8=2,得b=−5.又因为6+4+b+c=2,得c=−3,所以a+c+4+d=2,a+d=1.因为当a=−1时,d=2,则a+b=−1+(−5)=−6;当a=2时,d=−1,则a+b=2+(−5)=−3.
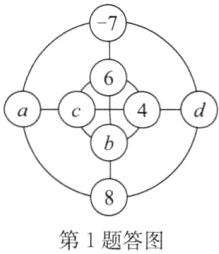
2. 如图,在一个由6个圆圈组成的三角形里,把1到6这6个数分别填入小圆圈内,使得三角形的每条边上的三个数的和$S$都相等,那么$S$的最大值是 ( )

A.9
B.10
C.12
D.13
答案:C 点拨:三角形的三个顶点处的数字是1~6这6个数中最大的三个数字,即三个顶点处分别是4,5,6,4与5 之间是3,6和5之间是1,4和6之间是2,这样每条边上的三个数的和才能相等.由答图可知S=3+4+5=12.

3. 观察下面的算式:$1+3= 4= 2^{2};1+3+5= 9= 3^{2};1+3+5+7= 16= 4^{2}……$
解答问题:
(1)$1+3+5+7+9+…+29= $
225
;
(2)若$n$表示正整数,则用含$n$的代数式表示上述规律为
$1+3+5+7+9+...+(2n−1)=n²$
;
(3)请用上述规律计算$41+43+45+47+49+…+2023+2025$的值(要求写出详细的解答过程).
解:因为2n−1=2025,所以n=1013,
所以原式=1+3+5+7+9+...+2023+2025−(1+3+5+7+9+..+39)=1013²−20²=1026169−400=1025769.
答案:(1)225
(2)1+3+5+7+9+...+(2n−1)=n²
(3)解:因为2n−1=2025,所以n=1013,
所以原式=1+3+5+7+9+...+2023+2025−(1+3+5+7+9+..+39)=1013²−20²=1026169−400=1025769.