1. 如图,$AB⊥MN$,$CD⊥MN$,垂足分别为$B和D$,$BE和DF分别平分∠ABN和∠CDN$. 下列结论:①$AB// CD$;②$∠1= ∠2$;③$CD⊥EF$;④$∠E+∠F= 180^{\circ}$. 其中结论正确的序号是(
C
)
A.①②③
B.②③④
C.①②④
D.①③④
答案:C 点拨:因为 AB⊥MN,CD⊥MN,所以∠ABN=∠CDN=90°,所以 AB//CD,故结论①正确.因为 BE 和 DF 分别平分∠ABN 和∠CDN,所以∠1= $\frac{1}{2}$∠ABN,∠2=$\frac{1}{2}$∠CDN,所以∠1=∠2,故结论②正确.因为 CD⊥MN,EF 与 MN 不一定平行,所以 EF 与 CD 不一定垂直,故结论③错误.因为∠1=∠2,所以 BE//DF,所以∠E+∠F=180°,故结论④正确.综上,结论正确的是①②④.
2. 如图,$GF⊥AB$,$∠1= ∠2$,$∠B= ∠AGH$,有下列结论:①$GH// BC$;②$∠D= ∠F$;③$HE平分∠AHG$;④$HE⊥AB$. 其中正确的是
①④
.(填序号)
答案:①④ 点拨:因为∠B=∠AGH,所以 GH//BC,即①正确;所以∠1=∠MGH.又因为∠1=∠2,所以∠2=∠MGH,所以 DE//GF.因为 GF⊥AB,所以 DE⊥AB,即④正确;∠D=∠F,HE 平分∠AHG 都不一定成立.
解析:
解:①④
∵∠B=∠AGH,
∴GH//BC(同位角相等,两直线平行),故①正确;
∴∠1=∠MGH(两直线平行,内错角相等),
∵∠1=∠2,
∴∠2=∠MGH(等量代换),
∴DE//GF(同位角相等,两直线平行),
∵GF⊥AB,
∴DE⊥AB(两直线平行,同位角相等),故④正确;
∠D=∠F,HE平分∠AHG无法证明,故②③错误。
综上,正确的是①④。
3. 如图,$AB// DG$,$AD// EF$.
(1)试说明:$∠1+∠2= 180^{\circ}$;
(2)若$DG是∠ADC$的平分线,$∠2= 138^{\circ}$,求$∠B$的度数.
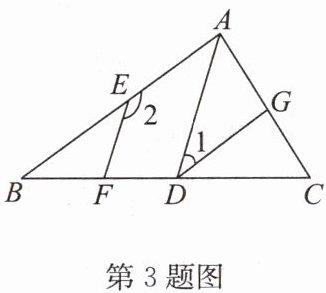
答案:(1)因为 AD//EF,所以∠BAD+∠2=180°.因为 AB//DG,所以∠BAD=∠1,所以∠1+∠2=180°.(2)因为∠1+∠2=180°且∠2=138°,所以∠1=42°.因为 DG 是∠ADC 的平分线,所以∠CDG=∠1=42°.因为 AB//DG,所以∠B=∠CDG=42°.
解析:
(1)∵AD//EF,
∴∠BAD+∠2=180°(两直线平行,同旁内角互补)。
∵AB//DG,
∴∠BAD=∠1(两直线平行,内错角相等)。
∴∠1+∠2=180°。
(2)∵∠1+∠2=180°,∠2=138°,
∴∠1=180°-∠2=180°-138°=42°。
∵DG是∠ADC的平分线,
∴∠CDG=∠1=42°。
∵AB//DG,
∴∠B=∠CDG=42°(两直线平行,同位角相等)。