1. 如图,下列条件:①$∠1= ∠2$;②$∠3+∠4= 180^{\circ }$;③$∠5+∠6= 180^{\circ }$;④$∠2= ∠3$;⑤$∠7= ∠2+∠3$;⑥$∠7+∠4-∠1= 180^{\circ }$. 其中能判定直线$a// b$的有 (
C
)
A.3个
B.4个
C.5个
D.6个
答案:C
解析:
解:①∵∠1=∠2,∠1与∠2是同位角,∴a//b;
②∵∠3+∠4=180°,∠3与∠4是同旁内角,∴a//b;
③∵∠5+∠6=180°,∠5=∠3(对顶角相等),∴∠3+∠6=180°,∠3与∠6是同旁内角,∴a//b;
④∵∠2=∠3,∠2与∠3是内错角,∴a//b;
⑤∵∠7=∠2+∠3,∠7=∠1+∠3(三角形外角性质),∴∠1=∠2,∠1与∠2是同位角,∴a//b;
⑥∵∠7+∠4-∠1=180°,∠7=∠1+∠3(三角形外角性质),∴∠1+∠3+∠4-∠1=∠3+∠4=180°,∠3与∠4是同旁内角,∴a//b。
综上,①②③④⑤⑥均能判定a//b,共6个。
答案:D
2. 将一副三角尺按如图放置,有下列结论:①$∠1= ∠3$;②若$∠2= 30^{\circ }$,则$AC// DE$;③若$∠2= 45^{\circ }$,则$BC// AD$;④若$∠4= ∠C$,则$∠2= 30^{\circ }$. 其中正确的有
①②③④
.(填序号)
答案:①②③④
解析:
解:①∵∠1+∠2=90°,∠3+∠2=90°,∴∠1=∠3,正确;
②若∠2=30°,则∠1=60°,∵∠E=60°,∴∠1=∠E,∴AC//DE,正确;
③若∠2=45°,则∠3=45°,∵∠B=45°,∴∠3=∠B,∴BC//AD,正确;
④∵∠C=30°,∠4=∠C=30°,∠EAD=90°,∴∠2=∠EAD - ∠4 - ∠3,又∠3=∠1=90° - ∠2,∴∠2=90° - 30° - (90° - ∠2),解得∠2=30°,正确。
正确的有①②③④。
3. 如图,在$∠MON的一边OM上有一点A$,另一边$ON上有一点C$,过点$A作ON$的垂线,交$ON于点B$,过点$C作OM$的垂线,交$OM于点D$,$AE$,$CF分别是∠DAB和∠DCB$的平分线,判断$AE与CF$是否平行,并说明理由.
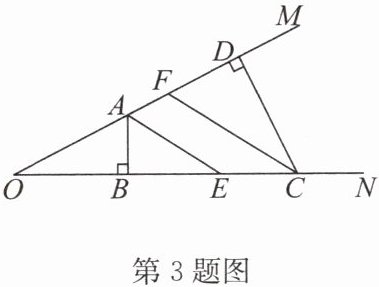
答案:解:AE//CF.理由:因为 AB⊥ON,CD⊥OM,所以∠ABE=∠CDF=90°,所以∠BAE+∠AEB=90°,∠BAD+∠DCB=180°.因为 AE,CF 分别是∠DAB 和∠DCB 的平分线,所以∠BAE=$\frac{1}{2}$∠DAB,∠FCE=$\frac{1}{2}$∠DCB,所以∠BAE+∠FCE=$\frac{1}{2}$∠DAB+$\frac{1}{2}$∠DCB=$\frac{1}{2}$(∠DAB+∠DCB)=90°,所以∠AEB=∠FCE,所以 AE//CF.