1. 如图,在长方形纸片 ABCD 中,M 为 AD 边上的一点,将纸片沿 BM,CM 折叠,使点 A 落在点$A_{1}$处,点 D 落在点$D_{1}$处.若$∠BMC= 105^{\circ }$,则$∠1$的度数为 ( )
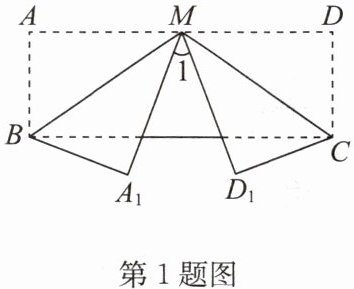
A.$60^{\circ }$
B.$75^{\circ }$
C.$45^{\circ }$
D.$30^{\circ }$
答案:D 点拨:如答图,由折叠的性质得∠2=∠3,∠4=∠5.因为∠BMC=105°,所以∠2+∠5=180°−∠BMC=75°,所以∠3+∠4=75°,所以∠1=∠BMC−(∠3+∠4)=105°−75°=30°.
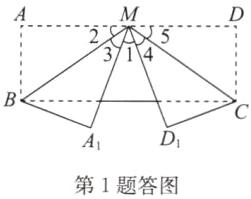
2. 如图,射线 OA 绕点 O 逆时针旋转一周,满足$∠EOF始终在∠AOB的内部且∠EOF= 58^{\circ }$.OM,ON 分别为$∠AOE和∠BOF$的平分线,在旋转过程中,$∠MON$的最大度数是____
119°
.
答案:119° 点拨:当∠AOB=180°时,∠MON的度数最大.因为∠EOF=58°,所以∠AOE+∠BOF=∠AOB−∠EOF=180°−58°=122°.
因为OM,ON分别为∠AOE和∠BOF的平分线,
所以∠MOE=$\frac{1}{2}$∠AOE,∠FON=$\frac{1}{2}$∠BOF,
所以∠MOE+∠FON=$\frac{1}{2}$(∠AOE+∠BOF)=$\frac{1}{2}$×122°=61°,所以∠MON=∠EOF+∠MOE+∠FON=58°+61°=119°,即∠MON的最大度数是119°.
3. 【定义】若$0^{\circ }<∠α<180^{\circ },0^{\circ }<∠β<180^{\circ }$,且$|∠α-∠β|= 45^{\circ }$,则称$∠α,∠β$互为“半余角”.如图,O 为直线 AB 上一点,$∠AOM= 15^{\circ },∠BON= 60^{\circ }$.
(1)图中的“半余角”有哪几对?
(2)若射线 ON 绕点 O 以每秒$10^{\circ }$的速度顺时针旋转,设旋转时间为 t 秒$(0<t<21).$
①当$t= 13.5$时,请判断$∠BON与∠MON$是否互为“半余角”,并说明理由;
②若射线 OM 同时绕点 O 以每秒$15^{\circ }$的速度顺时针旋转,当$∠AON与∠MON$互为“半余角”时,直接写出 t 的值.

答案:解:(1)有3对:∠AOM和∠BON,∠MON和∠BON,∠MOB和∠AON.理由如下:
因为∠AOM=15°,∠BON=60°,
所以∠MON=180°−∠AOM−∠BON=180°−15°−60°=105°,
所以|∠AOM−∠BON|=|15°−60°|=45°,
|∠MON−∠BON|=|105°−60°|=45°,
|∠MOB−∠AON|=|105°+60°−15°−105°|=45°.所以∠AOM和∠BON互为“半余角”,∠MON和∠BON 互为“半余角”,∠MOB和∠AON互为“半余角”.
(2)①是,理由:当t=13.5时,∠BON=10°×13.5−60°=75°,所以∠MON=15°+(180°−75°)=120°,
所以∠MON−∠BON=45°,
所以∠MON和∠BON互为“半余角”.
②2或18.