1. 如图,AB与CD交于点O,$∠AOE= 90^{\circ }$.
(1)若AB在东西方向上,点C在点O的南偏西$20^{\circ }$方向上,则点D在点O的
北偏东20°
方向上;
(2)若$∠EOD= 28^{\circ }$,求$∠AOC$的度数;
解:因为∠AOC+∠AOE+∠EOD=180°,∠EOD=28°,∠AOE=90°,所以∠AOC=180°-28°-90°=62°.
(3)若$∠AOC:∠BOC= 1:2$,求$∠EOD$的度数.
解:因为∠AOC:∠BOC=1:2,所以∠BOC=2∠AOC.因为∠AOC+∠BOC=180°,所以∠AOC+2∠AOC=180°,所以∠AOC=60°.因为∠AOC+∠AOE+∠EOD=180°,∠AOE=90°,所以∠EOD=30°.
答案:1.(1)北偏东20°
(2)解:因为∠AOC+∠AOE+∠EOD=180°,∠EOD=28°,∠AOE=90°,
所以∠AOC=180°-28°-90°=62°.
(3)解:因为∠AOC:∠BOC=1:2,
所以∠BOC=2∠AOC.
因为∠AOC+∠BOC=180°,
所以∠AOC+2∠AOC=180°,所以∠AOC=60°.
因为∠AOC+∠AOE+∠EOD=180°,∠AOE=90°,
所以∠EOD=30°.
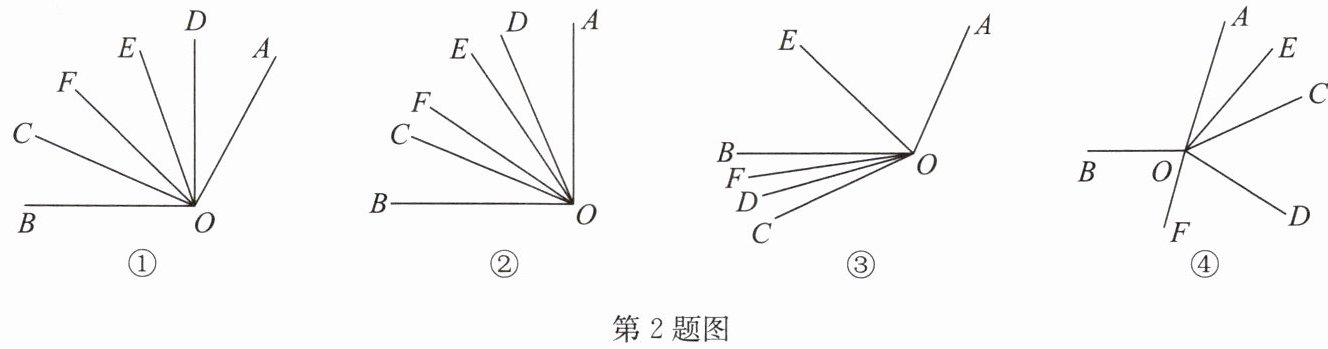
2. 如图①,已知$∠AOB和∠COD(∠COD<∠AOB),∠COD$绕着点O旋转,OE,OF分别是$∠AOC,∠BOD$的平分线.
(1)如图②,当$∠COD在∠AOB$的内部时,
①当$∠AOB= 90^{\circ },∠COD= 45^{\circ }$时,$∠EOF= $
22.5°
;
②当$∠AOB= 80^{\circ },∠EOF= 20^{\circ }$时,$∠COD= $
40°
.
(2)当$∠COD$在如图③的位置时,猜想$∠EOF与∠AOB,∠COD$的数量关系,并说明理由.
解:∠EOF=$\frac{1}{2}$(∠AOB-∠COD),理由如下:
设∠BOD=α,则∠AOC=α+∠AOB+∠COD.
因为OE,OF分别是∠AOC,∠BOD的平分线,
所以∠AOE=∠COE=$\frac{1}{2}$(α+∠AOB+∠COD),∠BOF=∠DOF=$\frac{1}{2}$α,
所以∠EOF=∠AOB-∠AOE+∠BOF=∠AOB-$\frac{1}{2}$(α+∠AOB+∠COD)+$\frac{1}{2}$α=∠AOB-$\frac{1}{2}$α-$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD+$\frac{1}{2}$α=$\frac{1}{2}$(∠AOB-∠COD).
(3)当$∠COD$在如图④的位置时,$∠EOF与∠AOB,∠COD$的数量关系是
∠EOF=180°-$\frac{1}{2}$(∠AOB-∠COD)
.
答案:2.(1)①22.5° 点拨:设∠AOD=x°,则∠BOC=(45-x)°,∠AOC=(45+x)°,∠BOD=(90-x)°.
因为OE,OF分别是∠AOC,∠BOD的平分线,
所以∠AOE=∠COE=$\frac{1}{2}$(45+x)°,∠BOF=∠DOF=$\frac{1}{2}$(90-x)°,
所以∠AOF=∠AOD+∠DOF=x°+$\frac{1}{2}$(90-x)°,
所以∠EOF=∠AOF-∠AOE=x°+$\frac{1}{2}$(90-x)°-$\frac{1}{2}$(45+x)°=22.5°.
②40° 点拨:设∠AOD=x°,∠BOC=y°,则∠AOC=(80-y)°,∠BOD=(80-x)°.
因为OE,OF分别是∠AOC,∠BOD的平分线,
所以∠AOE=∠COE=$\frac{1}{2}$(80-y)°,∠BOF=∠DOF=$\frac{1}{2}$(80-x)°.
因为∠BOF+∠EOF+∠AOE=∠AOB,
所以$\frac{1}{2}$(80-x)°+20°+$\frac{1}{2}$(80-y)°=80°,
所以x°+y°=40°,
所以∠COD=80°-(x+y)°=40°.
(2)解:∠EOF=$\frac{1}{2}$(∠AOB-∠COD),理由如下:
设∠BOD=α,则∠AOC=α+∠AOB+∠COD.
因为OE,OF分别是∠AOC,∠BOD的平分线,
所以∠AOE=∠COE=$\frac{1}{2}$(α+∠AOB+∠COD),∠BOF=∠DOF=$\frac{1}{2}$α,
所以∠EOF=∠AOB-∠AOE+∠BOF=∠AOB-$\frac{1}{2}$(α+∠AOB+∠COD)+$\frac{1}{2}$α=∠AOB-$\frac{1}{2}$α-$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD+$\frac{1}{2}$α=$\frac{1}{2}$(∠AOB-∠COD).
(3)∠EOF=180°-$\frac{1}{2}$(∠AOB-∠COD)
点拨:设∠AOC=β,则∠BOD=360°-∠AOB-∠COD-β.
因为OE,OF'分别是∠AOC,∠BOD的平分线,
所以∠AOE=∠COE=$\frac{1}{2}$β,∠BOF=∠DOF=$\frac{1}{2}$(360°-∠AOB-∠COD-β),
所以∠EOF=∠COE+∠COD+∠DOF=$\frac{1}{2}$β+∠COD+$\frac{1}{2}$(360°-∠AOB-∠COD-β)=$\frac{1}{2}$β+∠COD+180°-$\frac{1}{2}$∠AOB-$\frac{1}{2}$∠COD-$\frac{1}{2}$β=180°-$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠COD=180°-$\frac{1}{2}$(∠AOB-∠COD).