1. 如图,一个正方体骰子的六个面上分别标有1至6共六个数字,且相对面数字之和相同,将骰子按如图所示方式放置并按箭头方向无滑动翻转后停在M处,此时骰子朝上面的数字为(
D
)
A.3
B.4
C.5
D.6
答案:D
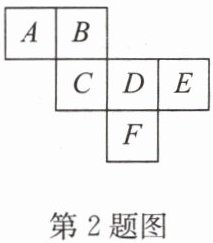
2. 如图是一个正方体的表面展开图,$A = x^{2}$,$B = 2x^{2} + 1$,$C = 2x - 2$,$D = 2x + 1$,且相对两个面所表示的整式的和都相等,则$E + F = $
2x+3
。
答案:2x+3 点拨:由正方体表面展开图的特点可知,标注“A”与“D”的面是相对的,标注“B”与“F”的面是相对的,标注“C”与“E”的面是相对的.又因为相对两个面所表示的整式的和都相等,所以A+D=B+F=C+E,所以E+F=2(A+D)-B-C=2x²+4x+2-(2x²+1)-(2x-2)=2x²+4x+2-2x²-1-2x+2=2x+3.
解析:
由正方体表面展开图特点可知:A与D相对,B与F相对,C与E相对。
因为相对两个面所表示的整式的和都相等,所以$A + D = B + F = C + E$。
$A + D = x^{2} + (2x + 1) = x^{2} + 2x + 1$
则$B + F = x^{2} + 2x + 1$,$C + E = x^{2} + 2x + 1$
$E + F = (C + E) + (B + F) - B - C$
$= 2(A + D) - B - C$
$= 2(x^{2} + 2x + 1) - (2x^{2} + 1) - (2x - 2)$
$= 2x^{2} + 4x + 2 - 2x^{2} - 1 - 2x + 2$
$= 2x + 3$
故答案为$2x + 3$。
3. 如图是一个正方体的表面展开图,标注了字母M的面是正方体的前面,标注了-2的面是正方体的底面,正方体的左面与右面标注的式子的和为21。(带式子的面朝外)
求:(1)x的值;
(2)正方体的上面和后面的数字的积。

答案:解:(1)由正方体表面展开图的特点可知,x与M所在面是相对的面,-2与-3所在面是相对的面,4x与2x+3所在面是相对的面.又因为标注了字母M的面是正方体的前面,标注了-2的面是正方体的底面,所以标注了字母x的面是正方体的后面,标注了-3的面是正方体的上面,因此标注了4x与2x+3的面是左面和右面,又因为正方体的左面与右面上标注的式子的和为21,所以4x+2x+3=21,解得x=3.
(2)因为标注了字母x的面是正方体的后面,标注了-3的面是正方体的上面,而x=3,所以正方体的上面和后面的数字的积为-3×3=-9.