21.(8分)如图,$AO\perp CO$,$BO\perp DO$,$\angle AOD = 145^{\circ}$,求$\angle BOC$的度数.
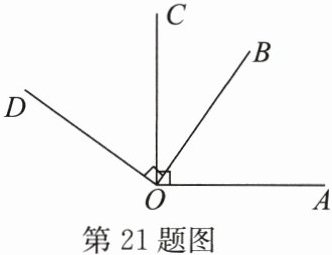
答案:解:因为AO⊥CO,BO⊥DO,所以∠AOC=∠BOD=90°.因为∠AOD=145°,所以∠BOC=∠AOC+∠BOD-∠AOD=90°+90°-145°=35°.
解析:
解:因为$AO\perp CO$,$BO\perp DO$,所以$\angle AOC = 90^\circ$,$\angle BOD=90^\circ$。
因为$\angle AOD = 145^\circ$,所以$\angle BOC=\angle AOC+\angle BOD-\angle AOD=90^\circ + 90^\circ-145^\circ=35^\circ$。
22.(8分)算“24”:用“1,2,6,7”4个有理数进行加、减、乘、除混合运算(每个数必须用一次且只能用一次,可以加括号),使得运算结果为“24”.请将算式写在下面的横线上.(注:用运算律改变算式的运算顺序属于同一个算式)
(1)
(7+1)×6÷2=24
; (2)
(1-7)×(2-6)=24
;
(3)
(7+6-1)×2=24
; (4)
6÷[2÷(1+7)]=24
.
答案:解:答案不唯一.例如:(1)(7+1)×6÷2=24. (2)(1-7)×(2-6)=24. (3)(7+6-1)×2=24. (4)6÷[2÷(1+7)]=24.
解析:
(1)$(7+1)×6÷2=24$
(2)$(1-7)×(2-6)=24$
(3)$(7+6-1)×2=24$
(4)$6÷[2÷(1+7)]=24$
23.(10分)解方程:
(1)$4(x - 1)= 1 - x$; (2)$\frac{x + 1}{2}= \frac{4}{3}x + 1$.
答案:解:(1)去括号,得4x-4=1-x,移项,得4x+x=1+4,合并同类项,得5x=5,系数化为1,得x=1. (2)去分母,得3(x+1)=8x+6,去括号,得3x+3=8x+6,移项,得3x-8x=6-3,合并同类项,得-5x=3,系数化为1,得x=$-\frac{3}{5}$.
24.(10分)如图,在四边形ABCD中,$AD// BC$,BD平分$\angle ABC$,$\angle A = 2\angle ABC$,$\angle C= \angle ABC$.
(1)求$\angle ADB$的大小;
(2)线段BD与DC有怎样的位置关系? 为什么?

答案:解:(1)因为AD//BC,所以∠A+∠ABC=180°.又因为∠A=2∠ABC,所以∠ABC=60°.因为BD平分∠ABC,所以∠DBC=$\frac{1}{2}$∠ABC=30°.因为AD//BC,所以∠ADB=∠DBC=30°. (2)BD⊥DC,理由如下:因为∠C=∠ABC=60°,∠DBC=30°,所以∠BDC=180°-∠DBC-∠C=90°,所以BD⊥DC.
解析:
(1)因为$AD// BC$,所以$\angle A + \angle ABC = 180^\circ$。又因为$\angle A = 2\angle ABC$,所以$2\angle ABC+\angle ABC = 180^\circ$,$3\angle ABC = 180^\circ$,$\angle ABC = 60^\circ$。因为$BD$平分$\angle ABC$,所以$\angle DBC=\frac{1}{2}\angle ABC = 30^\circ$。因为$AD// BC$,所以$\angle ADB=\angle DBC = 30^\circ$。
(2)$BD\perp DC$,理由如下:因为$\angle C=\angle ABC = 60^\circ$,$\angle DBC = 30^\circ$,所以$\angle BDC=180^\circ-\angle DBC-\angle C=180^\circ - 30^\circ - 60^\circ=90^\circ$,所以$BD\perp DC$。
25.(10分)已知$A = x^{2}-\frac{3}{2}xy + 2y^{2}$,$B = - 4x^{2}+3xy$,且$2A + B + C = 0$.
(1)求C;(用含x,y的代数式表示)
(2)若$\vert x + 2\vert+(y-\frac{1}{3})^{2}= 0$,求(1)中C的值.
答案:解:(1)因为2A+B+C=0,所以C=-2A-B.因为A=$x^{2}-\frac{3}{2}xy+2y^{2}$,B=$-4x^{2}+3xy$,所以C=$-2(x^{2}-\frac{3}{2}xy+2y^{2})-(-4x^{2}+3xy)=-2x^{2}+3xy-4y^{2}+4x^{2}-3xy=2x^{2}-4y^{2}$. (2)因为|x+2|+$(y-\frac{1}{3})^{2}=0$,所以x+2=0且$y-\frac{1}{3}=0$,所以x=-2,y=$\frac{1}{3}$,所以C=2×$(-2)^{2}-4×(\frac{1}{3})^{2}=2×4-4×\frac{1}{9}=8-\frac{4}{9}=\frac{68}{9}$.
26.(10分)某单位计划“双12”期间购进一批手写板,网上某店铺的标价为900元/台,优惠活动如下:
|购买数量|单价|
|不超过10台的部分|每台立减140元|
|超过10台但不超过20台的部分|每台立减220元|
|超过20台的部分|每台立减300元|
(1)①若该单位购买了16台这种手写板,花了
11680
元;
②若该单位购买了$x(x\gt20)$台这种手写板,花了
2400+600x
元.(用含x的代数式表示)
(2)若该单位购买的这种手写板的均价为696元,求他们购买的数量.
解:设他们购买了x台手写板.①当0<x≤10时,均价为760元,不合题意,舍去;②当10<x≤20时,费用为10×(900-140)+(900-220)(x-10)=680x+800,则680x+800=696x,解得x=50,不合题意,舍去;③当x>20时,有2400+600x=696x,解得x=25.综上,x的值为25.答:他们购买了25台手写板.
答案:(1)①11680 ②(2400+600x) (2)解:设他们购买了x台手写板.①当0<x≤10时,均价为760元,不合题意,舍去;②当10<x≤20时,费用为10×(900-140)+(900-220)(x-10)=680x+800,则680x+800=696x,解得x=50,不合题意,舍去;③当x>20时,有2400+600x=696x,解得x=25.综上,x的值为25.答:他们购买了25台手写板.