27.(12分)已知数轴上A,B两点表示的数分别为$-3$,1,P为数轴上任意一点,其表示的数为x.
(1)点A与点B之间的距离为
4
.
(2)若点P在点A与点B之间,则点P到点A的距离为
x+3
,点P到点B的距离为
1-x
,化简:$\vert x - 1\vert+\vert x + 3\vert=$
4
.
(3)若点P以每秒4个单位长度的速度从点A沿着数轴向右运动,同时点Q以每秒2个单位长度的速度从点B沿着数轴向右运动,同时点M以每秒1个单位长度的速度从点B沿着数轴向右运动.
①经过几秒,点P与点Q关于原点对称;
②经过
1或$\frac{8}{5}$或4
秒,P,Q,M三点中的任意两点关于另外一点对称.

①解:设运动t秒时,点P表示的数为-3+4t,点Q表示的数为1+2t,点P,Q关于原点对称时,-3+4t+1+2t=0,解得t=$\frac{1}{3}$.
答案:(1)4 (2)x+3 1-x 4 (3)①解:设运动t秒时,点P表示的数为-3+4t,点Q表示的数为1+2t,点P,Q关于原点对称时,-3+4t+1+2t=0,解得t=$\frac{1}{3}$. ②1或$\frac{8}{5}$或4
28.(12分)(2024·泗阳期末)定义:若$\angle\alpha = 2\angle\beta+\angle\gamma$,则称$\angle\alpha是\angle\beta$,$\angle\gamma$的加权伴随角.例如,$\angle\alpha = 50^{\circ}$,$\angle\beta = 20^{\circ}$,$\angle\gamma = 10^{\circ}$,此时$\angle\alpha = 2\angle\beta+\angle\gamma$,所以$\angle\alpha是\angle\beta$,$\angle\gamma$的加权伴随角.而$2\angle\gamma+\angle\beta = 40^{\circ}$,所以$\angle\alpha不是\angle\gamma$,$\angle\beta$的加权伴随角.
应用:(1)如果$\angle1 = 30^{\circ}$,$\angle2 = 40^{\circ}$,$\angle3 = 100^{\circ}$.
①$\angle3$______$\angle1$,$\angle2$的加权伴随角;
②$\angle3$______$\angle2$,$\angle1$的加权伴随角.(均填“是”或“不是”)
(2)如图,点O在直线AB上,C,D分别为射线OA,OB上的点,射线OC以每秒$10^{\circ}$的速度顺时针旋转,同时射线OD以每秒$15^{\circ}$的速度逆时针旋转,设旋转的时间为$t(0\lt t\lt12)$秒.
①当$t = 3$时,判断$\angle COD是否为\angle AOC$,$\angle BOD$的加权伴随角,并说明理由;
②若$\angle AOC = 2\angle COD$,求t的值;
③在$\angle AOC$,$\angle COD$,$\angle BOD$三个角中,若$\angle BOD$是另外两个角的加权伴随角,直接写出t的值.

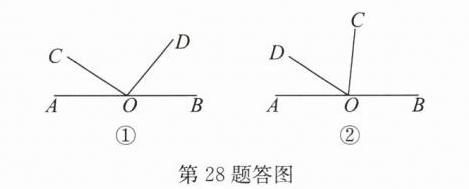
答案:(1)①是 ②不是 (2)解:①∠COD是∠AOC,∠BOD的加权伴随角,理由如下:当t=3时,∠AOC=30°,∠BOD=45°,∠COD=180°-30°-45°=105°,所以∠COD=2∠AOC+∠BOD,所以∠COD是∠AOC,∠BOD的加权伴随角. ②因为∠AOC=(10t)°,∠BOD=(15t)°,且∠AOC=2∠COD,所以当∠COD=180°-(25t)°时,10t=2(180-25t),解得t=6;当∠COD=(25t)°-180°时,10t=2(25t-180),解得t=9.综上,t的值为6或9. ③当0<t≤7.2时,如答图①,∠AOC=(10t)°,∠BOD=(15t)°,所以∠COD=180°-(25t)°.当∠BOD>∠COD时,若∠BOD=2∠AOC+∠COD,则15t=2×10t+180-25t,解得t=9>7.2,舍去;若∠BOD=2∠COD+∠AOC,则15t=2(180-25t)+10t,解得t=$\frac{72}{11}$;当7.2<t<12时,如答图②,∠AOC=(10t)°,∠BOD=(15t)°,∠COD=(25t)°-180°,此时∠BOD>∠COD,若∠BOD=2∠COD+∠AOC,则15t=2(25t-180)+10t,解得t=8;若∠BOD=2∠AOC+∠COD,则15t=2×10t+(25t-180),解得t=6<7.2,舍去.综上,t的值为$\frac{72}{11}$或8.
解析:
(1)①是 ②不是
(2)①∠COD是∠AOC,∠BOD的加权伴随角,理由如下:
当$t = 3$时,$\angle AOC=10^{\circ}×3 = 30^{\circ}$,$\angle BOD=15^{\circ}×3 = 45^{\circ}$,$\angle COD=180^{\circ}-30^{\circ}-45^{\circ}=105^{\circ}$,
$\because 2\angle AOC+\angle BOD=2×30^{\circ}+45^{\circ}=105^{\circ}=\angle COD$,
$\therefore \angle COD$是$\angle AOC$,$\angle BOD$的加权伴随角.
②$\angle AOC=(10t)^{\circ}$,$\angle BOD=(15t)^{\circ}$,
当$0\lt t\leq7.2$时,$\angle COD=180^{\circ}-(10t + 15t)^{\circ}=(180 - 25t)^{\circ}$,
$\because \angle AOC=2\angle COD$,$\therefore 10t=2(180 - 25t)$,解得$t = 6$;
当$7.2\lt t\lt12$时,$\angle COD=(10t + 15t - 180)^{\circ}=(25t - 180)^{\circ}$,
$\because \angle AOC=2\angle COD$,$\therefore 10t=2(25t - 180)$,解得$t = 9$;
综上,$t$的值为$6$或$9$.
③$\frac{72}{11}$或$8$