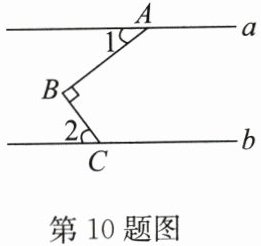
10. (2024·如东期中)如图,直线$a// b$,点$A在直线a$上,点$C在直线b$上,$AB⊥BC$.若$∠1= 35^{\circ }$,则$∠2= $
55
$^{\circ }$.
答案:55
11. (12分)计算:
(1)$3x+(-5x^{2})-(-2x)-5x$; (2)$1+(\frac {1}{2}-\frac {3}{4}-\frac {7}{8})×(-8)$.
答案:(1)原式=3x-5x²+2x-5x=-5x². (2)原式=1+$\frac{1}{2}$×(-8)-$\frac{3}{4}$×(-8)-$\frac{7}{8}$×(-8)=1-4+6+7=10.
12. (10分)解方程:
(1)$\frac {x+3}{2}-\frac {2x-3}{3}= 0$; (2)$5x-3(2x+3)= 8$.
答案:(1)去分母,得3(x+3)-2(2x-3)=0,去括号,得3x+9-4x+6=0,移项,得3x-4x=-9-6,合并同类项,得-x=-15,系数化为1,得x=15. (2)去括号,得5x-6x-9=8,移项、合并同类项,得-x=17,系数化为1,得x=-17.
13. (12分)(2024·宿城期中)已知$A= 2ab-a,B= -ab+2a+b$.
(1)计算:$5A-2B$;
(2)若$5A-2B的值与字母b$的取值无关,求$a$的值.
答案:(1)5A-2B=5(2ab-a)-2(-ab+2a+b)=10ab-5a+2ab-4a-2b=12ab-9a-2b. (2)因为5A-2B=12ab-9a-2b=(12a-2)b-9a的值与字母b的取值无关,所以12a-2=0,所以a=$\frac{1}{6}$.
14. (16分)已知一副三角尺按图①所示摆放,$∠AOB= ∠OCD= 90^{\circ },∠OAB= 45^{\circ },∠COD= 60^{\circ },OA,OC边重合在直线MN$上,$OB,OD边在直线MN$的两侧.
(1)保持$\triangle AOB$不动,将$\triangle COD绕点O$旋转至如图②所示的位置,则$∠BOC-∠AOD= $
30°
;
(2)保持$\triangle AOB$不动,将$\triangle COD绕点O逆时针旋转n^{\circ }(0\lt n\lt 180)$,试写出$∠BOC与∠AOD$的数量关系,不必说明理由;
解:当0<n≤60时,∠BOC-∠AOD=30°;当60<n≤90时,∠BOC+∠AOD=30°;当90<n<180时,∠AOD-∠BOC=30°
(3)如图③,若$\triangle COD按每分钟15^{\circ }的速度绕点O$逆时针旋转,同时,$\triangle AOB按每分钟9^{\circ }的速度也绕点O$逆时针旋转,多少分钟时,$OD边第一次与OB$边重合?
解:设x分钟时,OD边第一次与OB边重合,由题意,得15x-60=9x+90,解得x=25.答:25分钟时,OD边第一次与OB边重合.
答案:(1)30° (2)解:当0<n≤60时,∠BOC-∠AOD=30°;当60<n≤90时,∠BOC+∠AOD=30°;当90<n<180时,∠AOD-∠BOC=30° (3)解:设x分钟时,OD边第一次与OB边重合,由题意,得15x-60=9x+90,解得x=25.答:25分钟时,OD边第一次与OB边重合.
解析:
(1)$30^{\circ }$
(2)当$0\lt n\leqslant 60$时,$\angle BOC-\angle AOD=30^{\circ }$;当$60\lt n\leqslant 90$时,$\angle BOC+\angle AOD=30^{\circ }$;当$90\lt n\lt 180$时,$\angle AOD-\angle BOC=30^{\circ }$
(3)解:设$x$分钟时,$OD$边第一次与$OB$边重合,由题意,得$15x-60=9x+90$,解得$x=25$.答:$25$分钟时,$OD$边第一次与$OB$边重合.