11. (10分)计算:
(1)$ ( - 1 ) ^ { 2025 } × ( - 5 ) ÷ [ - 3 ^ { 2 } + ( - 2 ) ^ { 2 } ] $; (2)$ | - 12 | + ( - 3 ) ^ { 3 } - 3 × ( - 5 ) - 1 ^ { 2024 } $.
答案:解:(1)原式=5÷(-5)=-1. (2)原式=12-27+15-1=-1.
解析:
(1)解:原式$=(-1)×(-5)÷[-9 + 4]$
$=5÷(-5)$
$=-1$
(2)解:原式$=12+(-27)-(-15)-1$
$=12 - 27 + 15 - 1$
$=-1$
12. (10分)小明在计算多项式$ M 减去多项式 2 x ^ { 2 } y - 3 x y + 1 $时,误计算成加上这个多项式,结果得到答案$ 2 x ^ { 2 } y - x y $.
(1)请你帮小明求出多项式$ M $;
(2)对于(1)中的多项式$ M $,当$ x = - 1 $,$ y = 2 $时,求多项式$ M $的值.
答案:解:(1)由题意,得M+(2x²y-3xy+1)=2x²y-xy,所以M=2x²y-xy-(2x²y-3xy+1)=2x²y-xy-2x²y+3xy-1=2xy-1. (2)当x=-1,y=2时,M=2×(-1)×2-1=-4-1=-5.
解析:
(1)由题意,得$M+(2x^{2}y - 3xy + 1)=2x^{2}y - xy$,所以$M=2x^{2}y - xy-(2x^{2}y - 3xy + 1)=2x^{2}y - xy - 2x^{2}y + 3xy - 1=2xy - 1$。
(2)当$x=-1$,$y=2$时,$M=2×(-1)×2 - 1=-4 - 1=-5$。
13. (10分)已知$ A $,$ B $两件服装的成本共500元,某服装店老板分别以$ 30 \% 和 20 \% $的利润率定价后进行销售,该服装店共获利130元,问$ A $,$ B $两件服装的成本各是多少元?
答案:解:设A服装的成本为x元,则B服装的成本为(500-x)元.根据题意,得30%x+20%(500-x)=130,解得x=300,则500-x=200.答:A,B两件服装的成本分别为300元,200元.
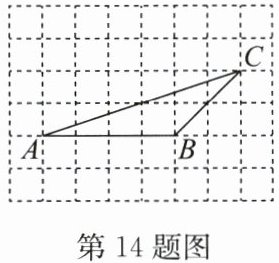
14. (10分)如图,在方格纸中,$ A $,$ B $,$ C $是三个格点(网格线的交点叫作格点).
(1)过点$ C 画 A B $的垂线,垂足为$ D $;
(2)将$ C D 沿 B C $翻折,得到直线$ C E $;
(3)直线$ C E 与直线 A B $的位置关系是______;
(4)判断:$ \angle A C B $______$ \angle A C E $. (填“$ > $”“$ < $”或“$ = $”)
答案:(1)解:如答图所示.
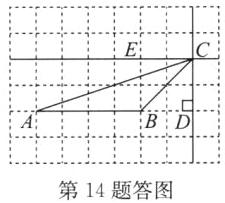
(2)解:如答图所示,直线CE即为所求. (3)平行 (4)>
15. (10分)(2024·宿城期末)如图,线段$ A B = 6 \mathrm { ~cm } $,延长$ B A 到点 C $,$ D 是线段 B C $的中点.
(1)若$ A C = 4 \mathrm { ~cm } $,求线段$ A D $的长.
解:因为AB=6cm,AC=4cm,所以BC=AB+AC=6+4=10(cm).因为D是BC的中点,所以CD=$\frac{1}{2}$BC=5(cm),所以AD=CD-AC=5-4=1(cm).即线段AD的长为1cm.
(2)若$ A C $的长逐渐增大,则$ A D $的长的变化趋势是
③
.(填序号)
①变小;②变大;③先变小,后变大;④先变大,后变小.
(3)若$ A D = 2 \mathrm { ~cm } $,求线段$ A C $的长.
解:当点D在线段AB上时,因为AB=6cm,AD=2cm,所以BD=AB-AD=6-2=4(cm).因为D是BC的中点,所以BC=2BD=2×4=8(cm),所以AC=BC-AB=8-6=2(cm).当点D在BA的延长线上时,因为AB=6cm,AD=2cm,所以BD=AB+AD=6+2=8(cm).因为D是BC的中点,所以BC=2BD=2×8=16(cm),所以AC=BC-AB=16-6=10(cm).综上,AC的长为2cm或10cm.
答案:(1)解:因为AB=6cm,AC=4cm,所以BC=AB+AC=6+4=10(cm).因为D是BC的中点,所以CD=$\frac{1}{2}$BC=5(cm),所以AD=CD-AC=5-4=1(cm).即线段AD的长为1cm. (2)③ (3)解:当点D在线段AB上时,因为AB=6cm,AD=2cm,所以BD=AB-AD=6-2=4(cm).因为D是BC的中点,所以BC=2BD=2×4=8(cm),所以AC=BC-AB=8-6=2(cm).当点D在BA的延长线上时,因为AB=6cm,AD=2cm,所以BD=AB+AD=6+2=8(cm).因为D是BC的中点,所以BC=2BD=2×8=16(cm),所以AC=BC-AB=16-6=10(cm).综上,AC的长为2cm或10cm.