3. 数学活动课上,老师带领学生们进行了折纸的系列综合实践活动.
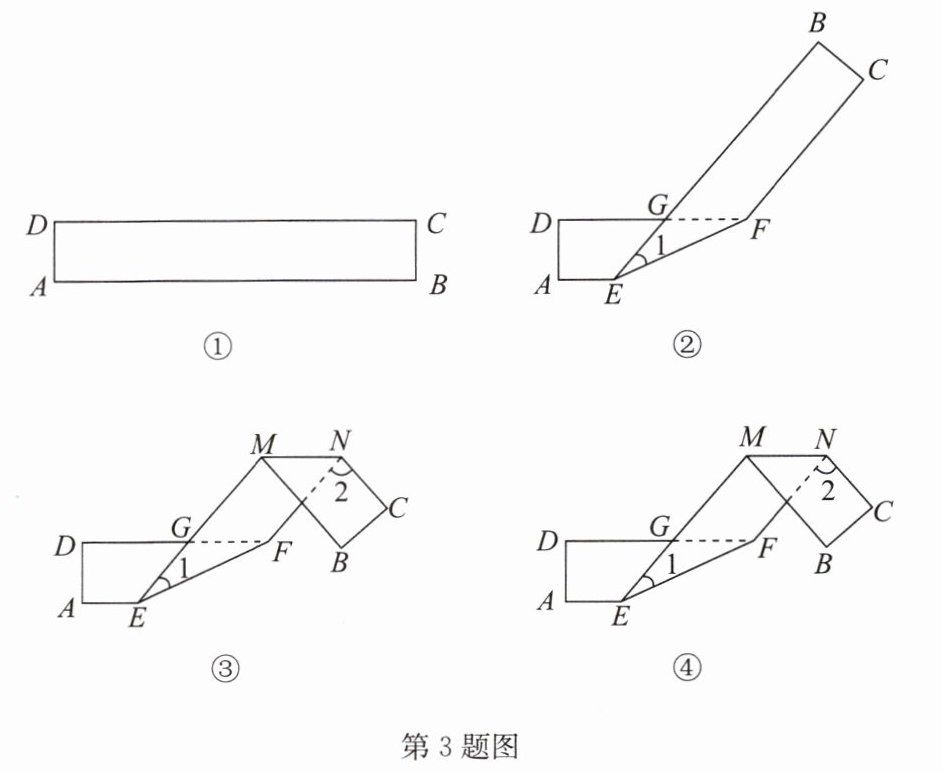
【活动素材】如图①,已知长方形纸片 ABCD($AB// CD$,$AD// BC$).
【活动 1】如图②,将长方形纸片 ABCD 进行折叠,沿 EF 折叠后 EB 与 DF 交于点 G,在探究过程中,同学们通过测量发现$∠1与∠GFE$的度数总是相等的;
【活动 2】如图③,在活动 1 的基础上,将长方形纸片 ABCD 进一步折叠,折痕为 MN,且$MN// AE$,同学们通过研究发现$∠1与∠2$之间也存在一定的数量关系;
【活动 3】如图④,在活动 2 的基础上,作$∠GFN$的平分线 FR,并反向延长与$∠FNC$的平分线交于点 Q,$∠Q与∠1$之间是否也存在确定的数量关系呢?
【任务 1】请说明:$∠GEF= ∠GFE;$
【任务 2】若$∠1= 25^{\circ }$,求$∠2$的度数;
【任务 3】依据活动 3,在图④中补全图形,并直接写出$∠Q与∠1$之间的数量关系.
答案:[任务1]如答图①,由折叠知∠FEB₁ = ∠FEB,
又因为AB₁//C₁D,
所以∠DFE = ∠FEB₁,所以∠GEF = ∠GFE;

[任务2]如答图①,由折叠可得∠GEB₁ = 2∠1 = 50°,
因为AB₁//C₁D,
所以∠DGE = ∠GEB₁ = 50°,
所以∠BGF = ∠DGE = 50°。
因为BE//CF,
所以∠CFG = 180°−∠BGF = 130°。
如答图②,因为MN//AE,FD//AE,
所以MN//FD,
所以∠MNF = 180°−∠GFN = 50°。
由MG//NF及折叠知,∠NMB = 50°。
因为MB//NC,所以∠MNC = 180°−∠NMB = 130°,所以∠2 = ∠MNC−∠MNF = 130°−50° = 80°。

[任务3]如答图①,由折叠可得∠GEB₁ = 2∠1,
因为AB₁//C₁D,
所以∠DGE = ∠GEB₁ = 2∠1,
所以∠BGF = ∠DGE = 2∠1。
因为BE//CF,
所以∠CFG = 180°−∠BGF = 180°−2∠1。
如答图②,因为MN//AE,FD//AE,
所以MN//FD,
所以∠MNF = 180°−∠NFG = 180°−(180°−2∠1) = 2∠1。由MG//NF及折叠知,∠NMB = 2∠1。
因为MB//NC,
所以∠MNC = 180°−∠NMB = 180°−2∠1,
所以∠2 = ∠MNC−∠MNF = 180°−2∠1−2∠1 = 180°−4∠1。
因为FR平分∠GFN,NQ平分∠FNC,
所以∠GFR = $\frac{1}{2}$∠GFN = $\frac{1}{2}$(180°−2∠1) = 90°−∠1,∠FNQ = $\frac{1}{2}$∠FNC = $\frac{1}{2}$(180°−4∠1) = 90°−2∠1,
所以∠MNQ = ∠MNF + ∠FNQ = 2∠1 + 90°−2∠1 = 90°。如答图②,过点Q作PQ//MN,则PQ//MN//DF,
所以∠PQR = ∠GFR = 90°−∠1,∠PQN = 180°−∠MNQ = 180°−90° = 90°。
所以∠RQN = ∠PQN−∠PQR = 90°−(90°−∠1) = ∠1。