1. 在一次数学实践活动课上,老师带领同学们探讨类似鸡蛋饼分割的问题.
(1)在一张圆形的彩纸上,如果画 6 条直线,最多可以把这张彩纸分成多少个区域?
(2)若将一张大饼看作一个平面,切 10 刀(每刀都是直线且大小不要求相同),最多能把大饼切成多少块?
(3)同学们在探讨过程中发现,直线分平面区域的规律和生活中很多场景类似. 比如在一个圆形的花园里,要设置若干条笔直的小路(看作直线),将花园分成不同的区域用来种植不同的花卉. 若已经设置了 3 条小路,现在要再设置 2 条小路,使花园被分成的区域最多,此时花园一共被分成了多少个区域?
答案:
(1)我们先找规律,设直线条数为n,最多分成的区域数为aₙ。
当n = 1时,a₁ = 2;
当n = 2时,a₂ = 4;
当n = 3时,a₃ = 7;
当n = 4时,a₄ = 11;
观察可得规律:aₙ = aₙ₋₁ + n(n≥2)。
那么a₅ = a₄ + 5 = 11 + 5 = 16;a₆ = a₅ + 6 = 16 + 6 = 22。所以画6条直线,最多可以把彩纸分成22个区域。
(2)由
(1)中规律可知
aₙ = 1 + 1 + 2 + 3 +... + n = 1 + $\frac{n(n + 1)}{2}$。
当n = 10时,a₁₀ = 1 + $\frac{10×11}{2}$ = 1 + 55 = 56。
所以切10刀最多能把大饼切成56块。
(3)由题意,得此时共设置5条小路,可看作平面上的5条直线,由
(1)知a₅ = 16。
故此时花园一共被分成了16个区域。
2. 在一次交通安全主题的数学综合实践活动中,同学们对汽车盲区问题进行了探究.
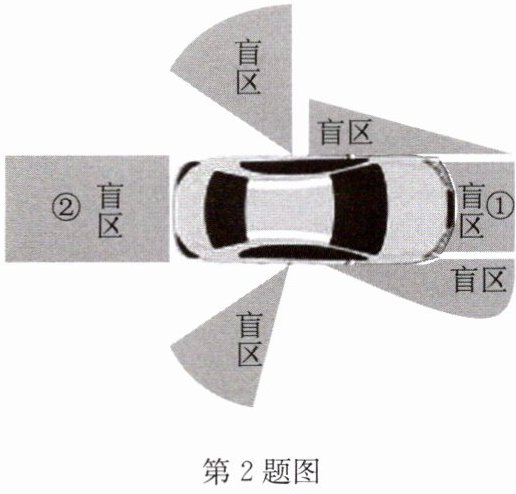
(1)已知一辆小型轿车的车长为 450 cm,车宽为 180 cm. 如图,盲区①近似为长方形,其长度为车长的$\frac{2}{3}$,宽度为车宽的$\frac{1}{2}$,求盲区①的面积;
(2)若另一辆 SUV 的车长为 480 cm,车宽为 200 cm,如图,盲区②也近似为长方形,其长度为车长的$\frac{3}{4}$,宽度为车宽的$\frac{3}{5}$,小型轿车盲区①的面积比这辆 SUV 盲区②的面积小多少平方厘米?
答案:
(1)由题意,得盲区①的长为450×$\frac{2}{3}$ = 300(cm)。宽为180×$\frac{1}{2}$ = 90(cm)。
所以盲区①的面积为300×90 = 27000(cm²)。
(2)对于SUV,车长为480cm,则盲区②的长为480×$\frac{3}{4}$ = 360(cm)。
车宽为200cm,则盲区②的宽为200×$\frac{3}{5}$ = 120(cm)。所以盲区②的面积为360×120 = 43200(cm²)。
小型轿车盲区①的面积比SUV盲区②的面积小43200 - 27000 = 16200(cm²)。