11. 如图, $ EG // AB,FG // DC, \angle B = 100 ^ { \circ }, \angle EGF = 40 ^ { \circ } $.求:(1) $ \angle EGC $ 的度数;(2) $ \angle C $ 的度数.
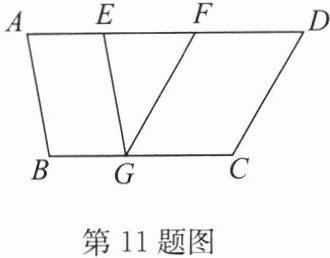
答案:解:
(1)因为EG//AB,∠B=100°,所以∠EGC=∠B=100°.
(2)因为∠EGC=100°,∠EGF=40°,所以∠FGC=∠EGC-∠EGF=100°-40°=60°.因为FG//CD,所以∠C+∠FGC=180°,所以∠C=120°.
12. (2024·宿城期中)如图①,直线 $ a,b $ 被直线 $ c $ 所截, $ \angle 1 $ 和 $ \angle 2 $ 在直线 $ c $ 的同一侧,且都不在直线 $ a,b $ 之间,具有这种位置关系的两个角叫做同旁外角.如图②, $ C,D $ 是直线 $ AB $ 上的两点,以 $ C,D $ 为端点作射线 $ CE,DF $.
(1)写出图②中的同旁外角;
(2)当 $ CE // DF $ 时,(1)中的同旁外角满足什么样的数量关系? 请说明理由.

答案:解:
(1)∠ACE和∠BDF.
(2)∠ACE+∠BDF=180°,理由如下:因为CE//DF(已知),所以∠ECD+∠CDF=180°(两直线平行,同旁内角互补).因为∠ACE+∠ECD=180°,∠BDF+∠CDF=180°(平角的定义),所以∠ACE=∠CDF,∠ECD=∠BDF(同角的补角相等),所以∠ACE+∠BDF=180°(等量代换).