6. (2024·海南)如图,直线 $ m // n $,把一块含 $ 45 ^ { \circ } $ 角的直角三角尺 $ ABC $ 按如图所示的方式放置,点 $ B $ 在直线 $ n $ 上, $ \angle A = 90 ^ { \circ } $.若 $ \angle 1 = 25 ^ { \circ } $,则 $ \angle 2 $ 等于 (
D
)
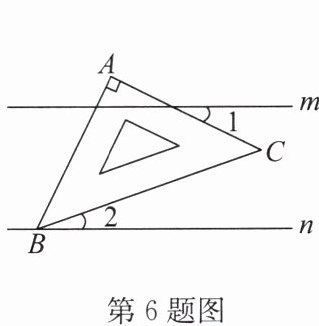
A.$ 70 ^ { \circ } $
B.$ 65 ^ { \circ } $
C.$ 25 ^ { \circ } $
D.$ 20 ^ { \circ } $
答案:D
解析:
延长AC交直线n于点D,
因为直线$m // n$,所以$\angle ADB = \angle 1 = 25^\circ$,
在$\triangle ABD$中,$\angle A = 90^\circ$,$\angle ADB = 25^\circ$,
所以$\angle ABD = 180^\circ - 90^\circ - 25^\circ = 65^\circ$,
因为$\triangle ABC$是含$45^\circ$角的直角三角尺,$\angle A = 90^\circ$,
所以$\angle ABC = 45^\circ$,
所以$\angle 2 = \angle ABD - \angle ABC = 65^\circ - 45^\circ = 20^\circ$
D
7. 如图, $ AB // CD,AD $ 平分 $ \angle BAC, \angle 1 = 30 ^ { \circ } $,则 $ \angle 2 = $ (
B
)
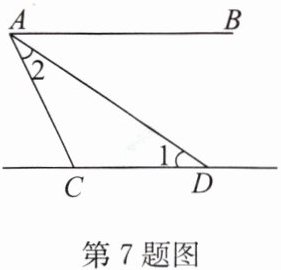
A.$ 15 ^ { \circ } $
B.$ 30 ^ { \circ } $
C.$ 45 ^ { \circ } $
D.$ 60 ^ { \circ } $
答案:B
解析:
∵AB//CD,∠1=30°,
∴∠BAD=∠1=30°(两直线平行,内错角相等)。
∵AD平分∠BAC,
∴∠2=∠BAD=30°。
B
8. (2024·呼伦贝尔)如图, $ AD // BC,AB \perp AC $.若 $ \angle 1 = 35.8 ^ { \circ } $,则 $ \angle B $ 的度数是 (
C
)

A.$ 35 ^ { \circ } 48 ^ { \prime } $
B.$ 55 ^ { \circ } 12 ^ { \prime } $
C.$ 54 ^ { \circ } 12 ^ { \prime } $
D.$ 54 ^ { \circ } 52 ^ { \prime } $
答案:C
解析:
∵AD//BC,
∴∠ACB=∠1=35.8°,
∵AB⊥AC,
∴∠BAC=90°,
∴∠B=180°-∠BAC-∠ACB=180°-90°-35.8°=54.2°,
∵0.2°=0.2×60'=12',
∴∠B=54°12',
C
9. (2024·深圳)如图,一束平行光线照射平面镜后反射,若入射光线与平面镜夹角 $ \angle 1 = 50 ^ { \circ } $,则反射光线与平面镜夹角 $ \angle 4 $ 的度数为 (
B
)

A.$ 40 ^ { \circ } $
B.$ 50 ^ { \circ } $
C.$ 60 ^ { \circ } $
D.$ 70 ^ { \circ } $
答案:B
解析:
根据光的反射定律,反射角等于入射角。
入射光线与平面镜夹角$\angle 1 = 50^\circ$,则入射角$\angle 2 = 90^\circ - \angle 1 = 90^\circ - 50^\circ = 40^\circ$,故反射角$\angle 3 = \angle 2 = 40^\circ$。
反射光线与平面镜夹角$\angle 4 = 90^\circ - \angle 3 = 90^\circ - 40^\circ = 50^\circ$。
B
10. 如图, $ AD $ 是 $ \angle BAC $ 的平分线,点 $ E $ 在 $ BC $ 上,点 $ F $ 在 $ CA $ 的延长线上, $ EF $ 交 $ AB $ 于点 $ G $,且 $ EF // AD $.试说明: $ \angle AGF = \angle F $.

答案:解:因为EF//AD,所以∠F=∠DAC,∠AGF=∠GAD.因为AD是∠BAC的平分线,所以∠GAD=∠DAC,所以∠AGF=∠F.