10. 下列说法:①任何数都有相反数;②符号不同的两个数互为相反数;③互为相反数的两个数绝对值相等;④0没有相反数. 其中正确的个数为(
B
)
A.1
B.2
C.3
D.4
答案:B
解析:
①任何数都有相反数,正确;
②符号不同的两个数互为相反数,错误(如$+2$与$-3$符号不同但不互为相反数);
③互为相反数的两个数绝对值相等,正确;
④0没有相反数,错误(0的相反数是0)。
正确的个数为2。
B
11. $x+2是-10$的相反数,则$x= $
8
.
答案:8
解析:
因为$-10$的相反数是$10$,由题意得$x + 2=10$,解得$x=8$。
12. 化简:
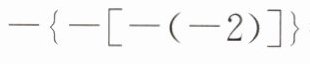
2
;$-\vert -2\vert=$
-2
.
答案:2 -2
13. (2024·建邺区期中)如图,点A,B在数轴上,若点A,B之间的距离为8,且A,B两点表示的数互为相反数,则点A表示的数为
-4
.

答案:-4
解析:
设点A表示的数为$x$,因为A,B两点表示的数互为相反数,所以点B表示的数为$-x$。
由数轴可知点B在点A右侧,所以$-x - x = 8$,即$-2x = 8$,解得$x = -4$。
$-4$
14. 已知$-[-(+x)]= 8$,则x的相反数是
-8
.
答案:-8
解析:
因为$-[-(+x)] = 8$,
先化简左边:$-[-(+x)] = -(-x) = x$,
所以$x = 8$,
则$x$的相反数是$-8$。
$-8$
15. 化简:(1)$-(-18)=$
18
;(2)$-[-(-\frac{3}{10})]=$
$-\frac{3}{10}$
;(3)$-[+(-0.67)]=$
0.67
.
答案:
(1)18
(2)$-\frac{3}{10}$
(3)0.67
16. 数轴上A,B两点表示的数互为相反数,且点A与点B之间的距离为4个单位长度,则点A表示的数是
2或-2
.
答案:2或-2
解析:
设点A表示的数为$x$,因为A,B两点表示的数互为相反数,所以点B表示的数为$-x$。
点A与点B之间的距离为$|x - (-x)| = |2x| = 4$,即$|2x| = 4$,解得$x = 2$或$x = -2$。
2或-2
17. 已知a与b互为相反数,b与c互为相反数,且$c= 2$,则$a= $
2
.
答案:2
解析:
因为a与b互为相反数,所以$a = -b$。
因为b与c互为相反数,所以$b = -c$。
则$a = -b = -(-c) = c$。
已知$c = 2$,所以$a = 2$。
2
18. 数轴上点A表示的数为$-3$,B,C两点表示的数互为相反数,且点B到点A的距离是2个单位长度,则点C表示的数是
1或5
.
答案:1或5
解析:
点A表示的数为$-3$,点B到点A的距离是2个单位长度,
当点B在点A左侧时,点B表示的数为$-3-2=-5$,
因为B,C两点表示的数互为相反数,所以点C表示的数是$5$;
当点B在点A右侧时,点B表示的数为$-3+2=-1$,
因为B,C两点表示的数互为相反数,所以点C表示的数是$1$;
综上,点C表示的数是$1$或$5$。
19. 化简下列各式,并回答问题:
$-(-8)$,$-(+8)$,$-[-(-8)]$,$-\{-[-(-8)]\}$.
(1)当$+8$的前面有2024个负号时,化简后的结果是多少?
(2)当$+8$的前面有2025个负号时,化简后的结果是多少?
(3)由上面的化简,你能得到什么规律?
答案:解:$-(-8)=8$,$-(+8)=-8$,$-[-(-8)]=-8$,$-\{-[-(-8)]\}=8$.
(1)8.
(2)-8.
(3)一个数的前面有奇数个负号时,化简后的结果等于它的相反数;一个数的前面有偶数个负号时,化简后的结果等于它本身.
20. 已知表示数a的点在数轴上的位置如图所示.
(1)在数轴上标出a的相反数对应的点的位置;
(2)若数a对应的点与其相反数对应的点相距10个单位长度,则$a= $______;
(3)在(2)的条件下,数b对应的点与数a对应的点相距2个单位长度,则$b= $______.

答案:(1)解:a的相反数对应的点的位置如答图所示.

(2)-5
(3)-7或-3