1.(2024·宿迁期末)如图,下列条件中,不能判定$AB// CD$的是(
D
)
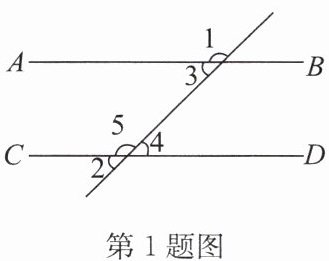
A.$∠3+∠5= 180^{\circ }$
B.$∠1= ∠5$
C.$∠3= ∠4$
D.$∠1= ∠2$
答案:D
2.(2024·兰州)如图,小明在地图上量得$∠1= ∠2$,由此判断幸福大街与平安大街互相平行,他判断的依据是(
B
)
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.对顶角相等
答案:B
3.如图,点E在BC的延长线上,则下列条件中,能判定$AD// BC$的是(
C
)

A.$∠B= ∠DCE$
B.$∠1= ∠2$
C.$∠3= ∠4$
D.$∠D+∠DAB= 180^{\circ }$
答案:C
4.如图,填空:
(1)因为$∠1= ∠2$,所以
AE
$// $
BD
,理由是
内错角相等,两直线平行
;
(2)因为$∠2= $
∠D
,所以$AC// DE$,理由是
同位角相等,两直线平行
;
(3)因为$∠1+∠E= 180^{\circ }$,所以
AC
$// $
DE
,理由是
同旁内角互补,两直线平行
.
答案:
(1)AE BD 内错角相等,两直线平行
(2)∠D 同位角相等,两直线平行
(3)AC DE 同旁内角互补,两直线平行
5.如图,下列条件:①$∠B+∠BCD= 180^{\circ }$;②$∠3= ∠4$;③$∠1= ∠2$;④$∠B= ∠5$.其中一定能判定$AB// CD$的是
①②④
.(填序号)
答案:①②④
6.如图,在三角形ABC中,$CD⊥AB$于点D,E是AC上一点,$∠1+∠2= 90^{\circ },DE$与BC平行吗?试说明理由.

答案:解:DE//BC.理由:因为CD⊥AB(已知),
所以∠1+∠3=90°(垂直的定义).
因为∠1+∠2=90°(已知),
所以∠3=∠2(同角的余角相等),
所以DE//BC(内错角相等,两直线平行).