1. 如图,直线 AB,CD 相交于点 O,EO⊥AB,垂足为 O. 若∠EOC = 40°,则∠AOD 的度数为(
C
)
A.110°
B.120°
C.130°
D.140°
答案:C
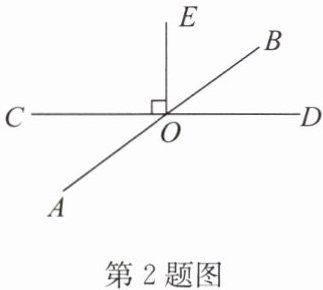
2. (2024·宿迁新区共同体期末)如图,直线 AB 与直线 CD 相交于点 O,EO⊥CD,垂足为 O. 若∠AOC = 35°24',则∠BOE 的度数为
54.6
°.
答案:54.6
解析:
∵直线AB与直线CD相交于点O,
∴∠AOC与∠BOD是对顶角,∠AOC=∠BOD=35°24'。
∵EO⊥CD,
∴∠EOD=90°。
∵∠BOE=∠EOD - ∠BOD,
∴∠BOE=90° - 35°24'=54°36'。
∵36'=36÷60=0.6°,
∴∠BOE=54.6°。
54.6
3. 如图,直线 AB,CD,EF 相交于点 O,AB⊥CD,∠DOE = 127°,求∠AOF 的度数.

答案:解:因为AB⊥CD,所以∠BOD=90°.
因为∠DOE=127°,
所以∠BOE=∠DOE-∠BOD=127°-90°=37°.
因为∠BOE=∠AOF,所以∠AOF=37°.
4. 如图,直线 AB,CD,EF 相交于点 O,EF⊥AB,OG 为∠COF 的平分线,若∠AOC : ∠COG = 4 : 7,求∠DOF 的度数.

答案:解:因为OG为∠COF的平分线,
所以∠COG=∠FOG.
因为∠AOC:∠COG=4:7,
所以设∠AOC=4x,∠COG=7x,则∠GOF=7x.
因为EF⊥AB,所以∠AOF=∠BOF=90°,
所以∠AOC+∠COG+∠GOF=90°,
即4x+7x+7x=18x=90°,
解得x=5°,
故∠AOC=∠DOB=20°,
则∠DOF=∠BOF+∠BOD=90°+20°=110°.