6. 下列说法:①直线AB与直线BA是同一条直线;②射线AB与射线BA是同一条射线;③两点确定一条直线;④同一平面内,经过一点有且只有一条直线与已知直线垂直;⑤两点之间的线段叫作两点之间的距离.其中正确的个数是 (
A
)
A.3
B.4
C.5
D.2
答案:A
解析:
①直线AB与直线BA是同一条直线,正确;
②射线AB与射线BA端点不同,不是同一条射线,错误;
③两点确定一条直线,正确;
④同一平面内,经过一点有且只有一条直线与已知直线垂直,正确;
⑤两点之间的线段的长度叫作两点之间的距离,错误。
正确的有①③④,共3个。
A
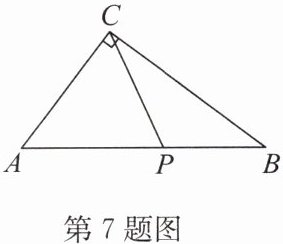
7. 如图,在三角形ABC中,$∠ACB= 90^{\circ },AC= 3,BC= 4,AB= 5$,P为直线AB上一动点,连接PC,则线段PC的最小值是 (
C
)
A.3
B.2.5
C.2.4
D.2
答案:C
解析:
在直角三角形中,垂线段最短。当$PC \perp AB$时,$PC$取得最小值。
已知在$\triangle ABC$中,$\angle ACB = 90^\circ$,$AC = 3$,$BC = 4$,$AB = 5$。
根据三角形面积公式,$S_{\triangle ABC} = \frac{1}{2} × AC × BC = \frac{1}{2} × AB × PC$。
即$\frac{1}{2} × 3 × 4 = \frac{1}{2} × 5 × PC$,
解得$PC = \frac{12}{5} = 2.4$。
C
8. 小聪和小颖是七年级(2)班的学生,在学习了《平面图形的初步认识》这一章内容后,他们开展了一项数学实践活动:小聪过点P作了直线PC和PD都垂直于直线AB,如图①所示;小颖用量角器作了两个角,其中$∠APB= 25^{\circ },∠BPC= 155^{\circ }$,如图②所示.小聪和小颖在一起讨论后,都说各自作图有错误,请聪明的你指出错在哪.

答案:解:小聪的错误在于过直线外一点有且只有一条直线垂直于已知直线,他作了两条;小颖的错误在于A,P,C三点应该在同一条直线上,因为∠APB+∠BPC=25°+155°=180°,即组成的∠APC是平角,而平角的两边在同一条直线上.
9. (2024·宿豫期末)已知AB是一条笔直的乡村道路,欲在道路上建一垃圾回收站.
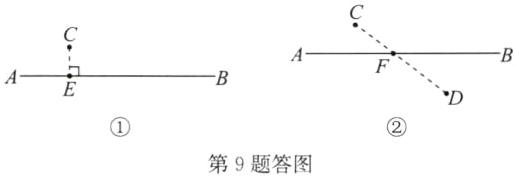
(1)如图①,如果垃圾回收站到C小区的距离最短,在图①中画出垃圾回收站E所建的位置.这样建的依据是______;
(2)如图②,如果在公路的另一侧还有小区D,如何确定垃圾回收站的位置,使其到两个小区的距离之和最短? 在图②中画出这个位置F,这样建的依据是______.

答案:解:
(1)如答图①,点E即为所求. 垂线段最短
(2)如答图②,点F即为所求. 两点之间,线段最短
10. 如图,直线AB,CD相交于点O,$OE⊥AB$.
(1)若$∠1= ∠2$,则OF与CD有什么位置关系? 请说明理由;
(2)若$∠2= \frac {1}{4}∠BOC$,求$∠AOC,∠DOE$的度数.

答案:解:
(1)OF⊥CD.理由如下:因为OE⊥AB(已知),所以∠AOE=∠AOC+∠2=90°(垂直的定义).因为∠1=∠2(已知),所以∠AOC+∠1=90°(等量代换),即∠COF=90°,所以OF⊥CD(垂直的定义).
(2)设∠2=x°.根据题意,得$x=\frac{1}{4}(90+x)$解得x=30,所以∠2=30°,所以∠AOC=90°-∠2=90°-30°=60°,∠DOE=180°-∠2=180°-30°=150°.