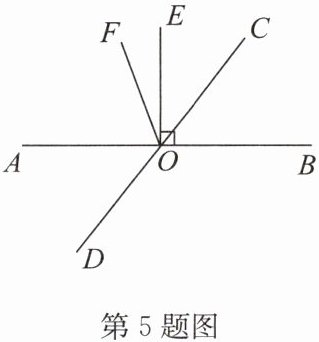
5. (2024·宿迁新区共同体期末)如图,直线 AB,CD 相交于点 O,OE⊥AB,垂足为 O,OF 平分∠AOC.
(1)若∠COE = 54°,求∠DOF 的度数;
(2)若∠COE : ∠EOF = 2 : 1,求∠DOF 的度数.
答案:
(1)因为OE⊥AB,所以∠AOE=90°.
因为∠COE=54°,所以∠AOC=∠AOE+∠COE=144°.
因为OF平分∠AOC,所以∠COF=$\frac{1}{2}$∠AOC=72°,
所以∠DOF=180°-∠COF=108°.
(2)设∠EOF=x°,则∠COE=2x°,所以∠COF=3x°.
因为OF平分∠AOC,所以∠AOF=∠COF=3x°,
所以∠AOE=4x°.
因为OE⊥AB,所以∠AOE=90°,所以4x=90,解得x=22.5,
所以∠COF=3x°=67.5°,
所以∠DOF=180°-∠COF=112.5°.
6. 如图,射线 OC,OD 在∠AOB 的内部,且∠AOC : ∠COD : ∠DOB = 2 : 3 : 4,射线 OM 平分∠AOC,射线 ON 平分∠BOD.
(1)若∠AOB = 144°,求∠COM 的度数;
(2)若 OM⊥ON,求∠COD 的度数.

答案:
(1)设∠AOC=2x,∠COD=3x,∠DOB=4x.
因为∠AOB=144°,所以2x+3x+4x=144°,
解得x=16°,
所以∠AOC=2x=32°.
因为OM平分∠AOC,所以∠COM=$\frac{1}{2}$∠AOC=16°.
(2)因为OM平分∠AOC,ON平分∠DOB,
所以∠MOC=$\frac{1}{2}$∠AOC=x,∠NOD=$\frac{1}{2}$∠BOD=2x,
所以∠MON=∠MOC+∠COD+∠DON=x+3x+2x=6x.
因为OM⊥ON,所以∠MON=90°,
所以6x=90°,解得x=15°,所以∠COD=45°.
7. 如图,O 为直线 AB 上一点,∠AOC = $\frac{1}{3}$∠BOC,OC 平分∠AOD. 试判断 OD 与 AB 的位置关系,并说明理由.

答案:解:OD⊥AB.理由如下:
因为O为直线AB上一点,所以∠AOC+∠BOC=180°.
又因为∠AOC=$\frac{1}{3}$∠BOC,
所以设∠AOC=x°,则∠BOC=(3x)°,
所以x+3x=180,解得x=45,所以∠AOC=45°.
因为OC平分∠AOD,所以∠AOD=2∠AOC=90°,
所以OD⊥AB.
8. 如图,O 是直线 AB 上一点,∠AOC = 40°,OD 平分∠AOC,∠COE = 70°.
(1)试说明:DO⊥OE;
(2)OE 平分∠BOC 吗?为什么?

答案:
(1)因为∠AOC=40°,OD平分∠AOC,
所以∠DOC=$\frac{1}{2}$∠AOC=20°.
因为∠COE=70°,
所以∠DOE=∠DOC+∠COE=20°+70°=90°,
所以DO⊥OE.
(2)OE平分∠BOC.
理由:因为∠AOC+∠COE+∠BOE=180°,
∠AOC=40°,∠COE=70°,
所以∠BOE=70°,所以∠BOE=∠COE,
所以OE平分∠BOC.