11. (10分)已知一个锐角的余角比这个锐角的补角的$\frac{1}{2}小20^{\circ}$,求这个锐角的度数.
答案:解:设这个锐角为x°.
根据题意,得90 - x = $\frac{1}{2}$(180 - x) - 20,解得x = 40.
这个锐角为40°.
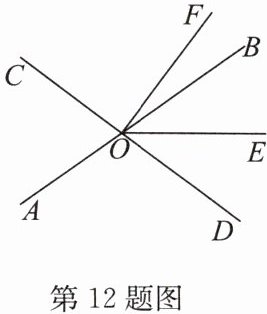
12. (10分)如图,直线AB,CD相交于点O,$\angle BOE = 36^{\circ}$,$\angle EOF = 54^{\circ}$,$\angle DOF = 90^{\circ}$.
(1)OE是$\angle BOD$的平分线吗? 为什么?
(2)求$\angle AOD$的度数.
答案:解:
(1)OE是∠BOD的平分线,理由如下:
因为∠EOF = 54°,∠DOF = 90°,
所以∠DOE = ∠DOF - ∠EOF = 90° - 54° = 36°.
又因为∠BOE = 36°,所以∠BOE = ∠DOE,
所以OE是∠BOD的平分线.
(2)因为∠AOD + ∠DOE + ∠BOE = 180°,
所以∠AOD = 180° - ∠DOE - ∠BOE = 180° - 36° - 36° = 108°.
13. (15分)如图,A,O,B三点在同一条直线上,$\angle BOD与\angle BOC$互补.
(1)$\angle AOC与\angle BOD$相等吗? 请说明理由.
(2)已知OM平分$\angle AOC$,射线ON在$\angle COD$的内部,且满足$\angle AOC与\angle MON$互余.
①若$\angle AOC = 32^{\circ}$,求$\angle MON$的度数;
②试探究$\angle AON与\angle DON$之间的数量关系,请写出结论并说明理由.

答案:解:
(1)∠AOC = ∠BOD.理由如下:
因为∠BOD与∠BOC互补,
所以∠BOD + ∠BOC = 180°.
因为∠AOC + ∠BOC = 180°,所以∠AOC = ∠BOD.
(2)①因为∠AOC与∠MON互余,
所以∠MON = 90° - ∠AOC = 90° - 32° = 58°.
②∠AON = ∠DON.理由如下:
如答图,

因为OM平分∠AOC,
所以∠AOC = 2∠AOM,∠COM = ∠AOM.
因为∠AOC与∠MON互余,
所以∠AOC + ∠MON = 90°,
所以∠AON = 90° - ∠AOM,
所以∠CON = ∠AON - ∠AOC = 90° - 3∠AOM.
因为∠BOD与∠BOC互补,
所以∠BOD + ∠BOC = 180°,
所以∠CON + ∠DON + 2∠BOD = 180°.
又因为∠BOD = ∠AOC = 2∠AOM,
所以∠DON = 180° - ∠CON - 2∠BOD
= ∠DON = ∠DON = 180° - (90° - ∠DON = 180° - (90° - 3∠AOM) - 4∠AOM
= 90° - ∠AOM,
所以∠AON = ∠DON;∠DON = 180° - (90° - 3∠AOM) - 4∠AOM
= 90° - ∠AOM,
所以∠AON = ∠DON;∠DON = 180° - (90° - ∠DON = 90° - ∠AOM,
所以∠AON = ∠DON;
14. (15分)(1)如图①,图中共有
2
对对顶角;如图②,图中共有
6
对对顶角;如图③,图中共有
12
对对顶角;
(2)猜想:若有n条直线相交于一点,则可形成
n(n - 1)
对对顶角;
(3)若有2023条直线相交于一点,则可形成
4090506
对对顶角.

答案:
(1)2 6 12
(2)n(n - )
(3)4090506