4. 如图,$∠AOB:∠BOC:∠COD = 2:3:4$,射线 OM,ON 分别平分$∠AOB和∠COD$,且$∠MON = 90^{\circ}$,求$∠BOD$的度数。
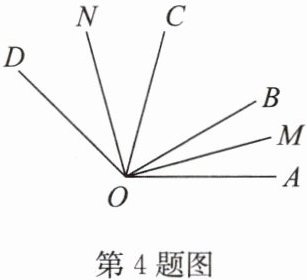
答案:解:设∠AOB=2α,则∠BOC=3α,∠COD=4α.
因为OM,ON分别平分∠AOB和∠COD,
所以∠BOM=$\frac{1}{2}$∠AOB=α,∠CON=$\frac{1}{2}$∠COD=2α.
因为∠MON=∠MOB+∠BOC+∠CON=90°,
所以α+3α+2α=90°,所以α=15°.
因为∠BOD=∠BOC+∠COD=3α+4α=7α,
所以∠BOD=105°.
5. (2024·姑苏区期末)如图,直线 AB,CD 相交于点 O,OE 平分$∠AOC$,OF 平分$∠BOE$,$∠AOD:∠COE = 4:1$,求$∠DOF$的度数。

答案:解:因为OE平分∠AOC,所以∠AOE=∠COE;
因为∠AOD:∠COE=4:1,所以设∠COE=x°,则∠AOE=x°,∠AOD=4x°.
因为∠COE+∠AOE+∠AOD=180°,
所以x+x+4x=180,解得x=30,
所以∠AOE=∠COE=30°,∠BOD=∠AOC=60°,
∠BOE=180°−∠AOE=150°.
因为OF平分∠BOE,所以∠BOF=$\frac{1}{2}$∠BOE=75°,所以∠DOF=∠DOB+∠BOF=60°+75°=135°.
6. (2024·金坛区期末)已知 OC 是$∠AOB$的平分线,$∠BOD = \frac{1}{3}∠COD$,OE 平分$∠COD$。设$∠AOB = \alpha$,则$∠BOE = $ (
A
)
A.$\frac{5}{16}\alpha或\frac{1}{8}\alpha$
B.$\frac{5}{16}\alpha或\frac{1}{6}\alpha$
C.$\frac{1}{8}\alpha或\frac{1}{6}\alpha$
D.$\frac{1}{6}\alpha$
答案:A
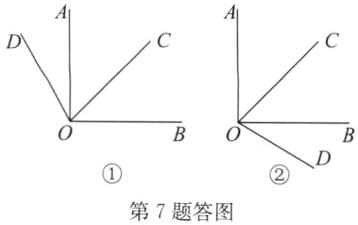
7. 如图,$∠AOB = 90^{\circ}$,OC 平分$∠AOB$。若$∠COD = 75^{\circ}$,请补全图形,并求出$∠BOD$的度数。

答案:解:因为∠AOB=90°,OC平分∠AOB,
所以∠AOC=∠BOC=$\frac{1}{2}$∠AOB=45°.
由,题意可知OD在图中的位置有两种情况,如答图①,②所示
如答图①,∠BOD=∠BOC+∠COD=45°+75°=120°;如答图②,∠BOD=∠COD−∠BOC=75°−45°=30°.
综上,∠BOD的度数为120°或30°.