1. 下列各图中,$∠1和∠2$是对顶角的是 (
B
)
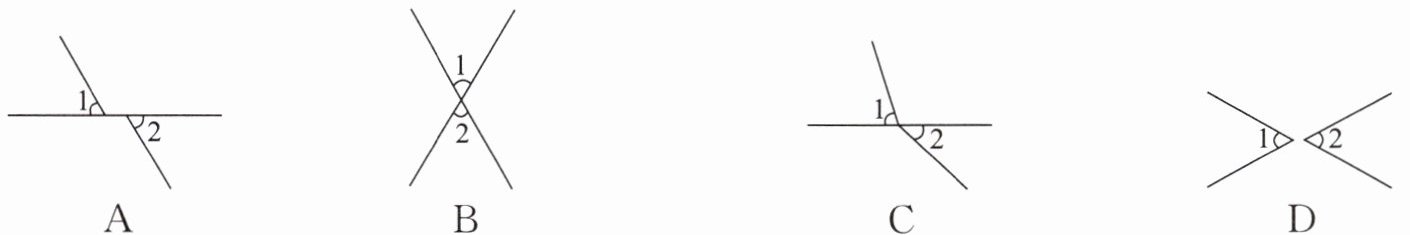
答案:B
2. (2024·宿城期末)泰勒斯被誉为古希腊及西方第一个自然科学家和哲学家,据说“两条直线相交,对顶角相等”就是泰勒斯首次发现并论证的. 论证“对顶角相等”使用的依据是 (
B
)
A.同角的余角相等
B.同角的补角相等
C.等角的余角相等
D.等角的补角相等
答案:B
3. (2024·浦口区期末)如图,直线 AB,CD 相交于点$O$,$OA平分∠COE$. 若$∠BOD= 30^{\circ }$,则图中大小为$60^{\circ }$的角是 (
A
)

A.$∠COE$
B.$∠EOD$
C.$∠COB$
D.$∠BOE$
答案:A
解析:
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=30°(对顶角相等)。
∵OA平分∠COE,
∴∠COE=2∠AOC=2×30°=60°。
A
4. (2024·广西改编)已知$∠1与∠2$为对顶角,$∠1+∠2= 70^{\circ }$,则$∠2=$
35
$^{\circ }$.
答案:35
解析:
∵∠1与∠2为对顶角,
∴∠1=∠2,
∵∠1+∠2=70°,
∴∠2+∠2=70°,
∴2∠2=70°,
∴∠2=35°。
35
5. 如图,直线 AB,CD 相交于点$O$,$∠AOC= 90^{\circ }$,下列说法:①图中对顶角有 2 对,邻补角有 4 对;②$∠AOD与∠BOD$互补且相等;③$∠AOC与∠BOC$是对顶角;④图中四个角相等,且每个角与其他的角互补. 其中错误的是______
③
. (填序号)
答案:③
6. 如图,直线 AB,CD 相交于点$O$,$OE平分∠BOD$,$∠BOE= 36^{\circ }$. 求$∠AOC$的度数.

答案:解:因为OE平分∠BOD,∠BOE=36°,
所以∠BOD=2∠BOE=2×36°=72°。
因为直线AB,CD相交于点O,
所以∠AOC与∠BOD是对顶角,
所以∠AOC=∠BOD=72°。