7. 如图,∠AOB是直角,∠AOC= 38°,∠COD:∠COB= 1:2,则∠DOB= (
C
)
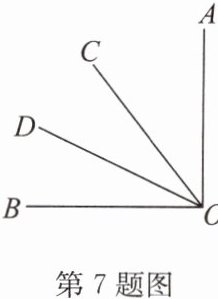
A.38°
B.52°
C.26°
D.64°
答案:C
解析:
∵∠AOB是直角,
∴∠AOB=90°,
∵∠AOC=38°,
∴∠COB=∠AOB - ∠AOC=90° - 38°=52°,
∵∠COD:∠COB=1:2,
∴∠COD= $\frac{1}{2}$∠COB= $\frac{1}{2}×52°=26°$,
∵点D在∠COB内部,
∴∠DOB=∠COB - ∠COD=52° - 26°=26°。
C
8. (2024·仪征期末)小正方形网格如图所示,A,B,C,D,O均为格点,那么∠AOB
>
∠COD。(填“>”“<”或“=”)

答案:>
解析:
设每个小正方形边长为1。
在$Rt\triangle ABO$中,$AB = 1$,$BO = 1$,$\tan\angle AOB=\frac{AB}{BO}=\frac{1}{1}=1$,则$\angle AOB = 45^\circ$。
在$Rt\triangle CDO$中,$CD = 2$,$DO = 3$,$\tan\angle COD=\frac{CD}{DO}=\frac{2}{3}$。
因为$\tan45^\circ = 1>\frac{2}{3}$,且正切函数在$(0^\circ,90^\circ)$单调递增,所以$\angle AOB>\angle COD$。
>
9. 如图,直线AB,CD相交于点O,OE平分∠AOD,若∠BOD= 100°,则∠AOE=
40°
。

答案:40°
解析:
∵直线AB,CD相交于点O,∠BOD=100°,
∴∠AOD=180° - ∠BOD=180° - 100°=80°。
∵OE平分∠AOD,
∴∠AOE=∠AOD×$\frac{1}{2}$=80°×$\frac{1}{2}$=40°。
40°
10. 如果一艘轮船航行到C处观测小岛A的方向是北偏西52°,那么同时在A处观测轮船的方向是
南偏东52°
。
答案:南偏东52°
11. (2024·钟楼区期末)已知∠AOB= 60°,OM是∠AOB的平分线,∠BOC= 20°,ON是∠BOC的平分线,则∠MON的度数为
40°或20°
。
答案:40°或20°
解析:
情况1:OC在∠AOB内部
∵OM平分∠AOB,∠AOB=60°,
∴∠BOM=∠AOB/2=30°。
∵ON平分∠BOC,∠BOC=20°,
∴∠BON=∠BOC/2=10°。
∴∠MON=∠BOM-∠BON=30°-10°=20°。
情况2:OC在∠AOB外部
∵OM平分∠AOB,∠AOB=60°,
∴∠BOM=∠AOB/2=30°。
∵ON平分∠BOC,∠BOC=20°,
∴∠BON=∠BOC/2=10°。
∴∠MON=∠BOM+∠BON=30°+10°=40°。
20°或40°
12. 如图,点O在直线AB上,∠AOE:∠EOD= 1:3,OC是∠BOD的平分线,∠EOC= 115°,求∠AOE和∠BOC的度数。

答案:解:由∠AOE:∠EOD=1:3,可设∠AOE=x°,则∠EOD=(3x)°.因为∠EOC=115°,所以∠COD=(115-3x)°.因为 OC 是∠BOD 的平分线,所以∠BOC=∠COD=(115-3x)°.因为点 O 在直线 AB 上,所以x+115+115-3x=180,所以x=25,所以∠AOE=25°,∠BOC=(115-3x)°=40°.
解析:
解:设$\angle AOE = x^{\circ}$,由$\angle AOE:\angle EOD = 1:3$,得$\angle EOD = 3x^{\circ}$。
因为$\angle EOC = 115^{\circ}$,所以$\angle COD=\angle EOC-\angle EOD=(115 - 3x)^{\circ}$。
因为$OC$是$\angle BOD$的平分线,所以$\angle BOC=\angle COD=(115 - 3x)^{\circ}$。
由于点$O$在直线$AB$上,$\angle AOB = 180^{\circ}$,则$\angle AOE+\angle EOC+\angle BOC=180^{\circ}$,即$x + 115+(115 - 3x)=180$。
解得$x = 25$,所以$\angle AOE=25^{\circ}$,$\angle BOC=(115 - 3×25)^{\circ}=40^{\circ}$。
答:$\angle AOE$的度数为$25^{\circ}$,$\angle BOC$的度数为$40^{\circ}$。
13. 如图,∠AOB= 90°,∠BOC= 30°,OM平分∠AOC,ON平分∠BOC。
(1)求∠MON的度数;
(2)若将题目中的∠AOB= 90°改为∠AOB= α,其余条件不变,求∠MON的度数;
(3)若将题目中的∠BOC= 30°改为∠BOC= β(β为锐角),其余条件不变,求∠MON的度数;
(4)归纳:从(1)(2)(3)中,你能得出什么结论?

答案:解:
(1)因为 OM 平分∠AOC,ON 平分∠BOC,所以$∠MOC=\frac {1}{2}∠AOC,∠NOC=\frac {1}{2}∠BOC.$又因为∠AOB=90°,所以$∠MON=∠MOC-∠NOC=\frac {1}{2}∠AOC-\frac {1}{2}∠BOC=\frac {1}{2}(∠AOC-∠BOC)=\frac {1}{2}∠AOB=\frac {1}{2}×90°=45°.(2)$当∠AOB=α,其余条件不变时$,∠MON=\frac {1}{2}∠AOB=\frac {1}{2}α.(3)$当∠BOC=β,其余条件不变时$,∠MON=\frac {1}{2}∠AOB=\frac {1}{2}×90°=45°.(4)$由
(1)
(2)
(3)的结果,可得出结论:∠MON 总等于∠AOB 的一半,而与∠BOC 的大小无关.