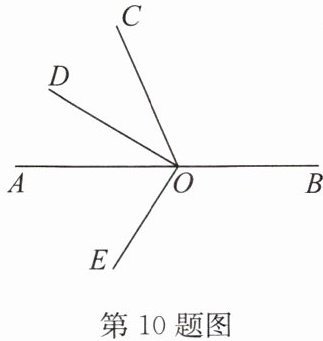
10. (2024·南师附中宿迁分校期末)如图,$∠AOB$是平角,OD是$∠AOC$的平分线,$∠COE= ∠BOE$.当$∠COD=$
45°
时,与$∠COD$互补的角有3个.
答案:45°
解析:
设$∠COD = x$。
因为OD是$∠AOC$的平分线,所以$∠AOC = 2∠COD = 2x$。
因为$∠AOB$是平角,所以$∠COB = 180^{\circ}-∠AOC = 180^{\circ}-2x$。
因为$∠COE = ∠BOE$,所以$∠COE = ∠BOE=\frac{1}{2}∠COB=\frac{1}{2}(180^{\circ}-2x)=90^{\circ}-x$。
与$∠COD$互补的角满足和为$180^{\circ}$,则:
$∠AOD + ∠DOB = 180^{\circ}$,但$∠AOD = ∠COD = x$,所以$∠DOB = 180^{\circ}-x$,是互补角;
$∠AOC + ∠COB = 180^{\circ}$,$∠COB = 180^{\circ}-2x$,若$180^{\circ}-2x = 180^{\circ}-x$,则$x = 0^{\circ}$,不成立;
$∠AOE$:$∠AOE = 180^{\circ}-∠BOE = 180^{\circ}-(90^{\circ}-x)=90^{\circ}+x$,若$90^{\circ}+x = 180^{\circ}-x$,则$2x = 90^{\circ}$,$x = 45^{\circ}$;
$∠DOE$:$∠DOE = ∠DOC + ∠COE = x + (90^{\circ}-x)=90^{\circ}$,不是;
$∠AOE = 90^{\circ}+x$,当$x = 45^{\circ}$时,$∠AOE = 135^{\circ}$,$180^{\circ}-45^{\circ}=135^{\circ}$,是互补角;
$∠COB = 180^{\circ}-2x$,当$x = 45^{\circ}$时,$∠COB = 90^{\circ}$,不是;
$∠AOD = x$,其补角为$180^{\circ}-x$,此时$∠DOB = 180^{\circ}-x$,$∠AOE = 135^{\circ}=180^{\circ}-45^{\circ}$,还有$∠DOE$若为$135^{\circ}$,则$90^{\circ}-x + x = 90^{\circ}$,不是,实际此时互补角为$∠DOB$、$∠AOE$、$∠COE$的补角等,经分析当$x = 45^{\circ}$时,有$∠DOB$、$∠AOE$、$∠COE$的对顶角等共3个互补角。
综上,$x = 45^{\circ}$。
$45^{\circ}$
11. 如图,直线CD经过点O,且$∠AOC= ∠BOC,∠AOD与∠BOD$有怎样的大小关系?为什么?

答案:解:$∠AOD=∠BOD$.理由如下:
因为直线 CD 经过点 O,
所以$∠COD=∠AOC+∠AOD=∠BOC+∠BOD=180^{\circ }$.
因为$∠AOC=∠BOC$,
所以$∠AOD=∠BOD$(等角的补角相等).
12. 如图,点A,O,B在同一条直线上,$∠1+∠2= 90^{\circ },∠COD= 90^{\circ }$.
(1)请写出图中相等的角,并说明理由;
(2)请直接写出图中互余的角和互补的角.

答案:
(1)题图中相等的角有$∠2=∠AOC,∠BOC=∠BOE$.理由如下:
因为点 A,O,B 在同一条直线上,
所以$∠AOB=∠AOC+∠COD+∠1=∠2+∠BOE=180^{\circ }$.
因为$∠COD=90^{\circ }$,所以$∠AOC+∠1=90^{\circ }$.
又因为$∠1+∠2=90^{\circ }$,所以$∠2=∠AOC$(同角的余角相等).
又因为$∠2+∠BOE=∠AOC+∠BOC=180^{\circ },$
所以$∠BOE=∠BOC$(等角的补角相等).
(2)$∠1$与$∠2$互余,$∠AOC$与$∠1$互余;$∠1$与$∠AOD$互补,$∠2$与$∠BOE$互补,$∠2$与$∠BOC$互补,$∠AOC$与$∠BOC$互补,$∠AOC$与$∠BOE$互补.
13. 如图,$∠AOC= ∠BOD= 90^{\circ }$.
(1)$∠AOD$
=
$∠BOC$(填“>”“<”或“=”),理由是
同角的余角相等
;
(2)若$∠AOB= 140^{\circ }$,则$∠COD= $
40
$^{\circ }$;
(3)如果$∠AOB= n^{\circ }(n<180)$,求$∠COD$的度数;(用含n的代数式表示)
解:因为$∠AOC=∠BOD=90^{\circ },$
所以$∠AOC+∠BOD=∠AOD+∠COD+∠BOC+∠COD=∠AOB+∠COD=180^{\circ }$.
又因为$∠AOB=n^{\circ },$
所以$∠COD=180^{\circ }-∠AOB=180^{\circ }-n^{\circ }$.
(4)图中互补的角有:
$∠AOC$与$∠BOD,∠AOB$与$∠COD$
.
答案:
(1)= 同角的余角相等
(2)40
(3)解:因为$∠AOC=∠BOD=90^{\circ },$
所以$∠AOC+∠BOD=∠AOD+∠COD+∠BOC+∠COD=∠AOB+∠COD=180^{\circ }$.
又因为$∠AOB=n^{\circ },$
所以$∠COD=180^{\circ }-∠AOB=180^{\circ }-n^{\circ }$.
(4)$∠AOC$与$∠BOD,∠AOB$与$∠COD$