1. (2024·武威)若$∠A= 55^{\circ }$,则$∠A$的补角为(
D
)
A.$35^{\circ }$
B.$45^{\circ }$
C.$115^{\circ }$
D.$125^{\circ }$
答案:D
解析:
因为互为补角的两个角的和为$180^{\circ}$,所以$\angle A$的补角为$180^{\circ}-\angle A = 180^{\circ}-55^{\circ}=125^{\circ}$。
D
2. (2024·吴江区期末)若$∠1= 43^{\circ }$,则$∠1$的余角是(
B
)
A.$43^{\circ }$
B.$47^{\circ }$
C.$57^{\circ }$
D.$137^{\circ }$
答案:B
解析:
$90^{\circ}-43^{\circ}=47^{\circ}$,故选B。
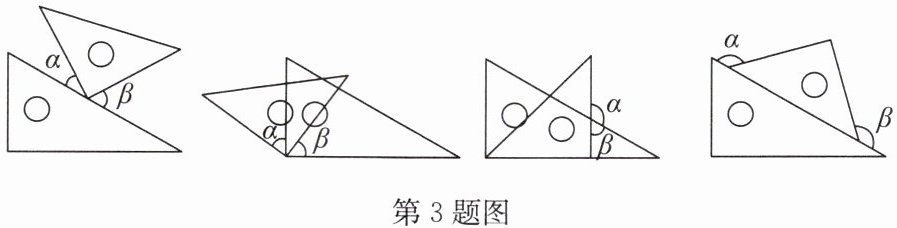
3. 如图,一副三角尺按不同的位置摆放,其中$∠α与∠β$一定相等的图形有(
C
)
A.4个
B.3个
C.2个
D.1个
答案:C
4. 下列说法:①如果$∠A= 40^{\circ },∠B= 50^{\circ },∠C= 90^{\circ }$,那么$∠A,∠B,∠C$互为补角;②互补的两个角中,至少有一个角大于或等于直角;③锐角的余角还是锐角;④两个互补的角中必有一个是钝角,其中正确的有(
B
)
A.1个
B.2个
C.3个
D.4个
答案:B
解析:
①补角是两个角之间的关系,三个角不能互为补角,错误;
②互补的两个角和为$180^{\circ}$,若两个角都小于直角($90^{\circ}$),则和小于$180^{\circ}$,故至少有一个角大于或等于直角,正确;
③锐角小于$90^{\circ}$,其余角为$90^{\circ}-$锐角,结果仍小于$90^{\circ}$,是锐角,正确;
④两个直角互补,此时没有钝角,错误。
正确的有②③,共2个。
B
5. 一个角的余角与这个角的补角也互为补角,这个角的度数是
45°
;互为余角且相等的两个角的度数是
45°,45°
;互为补角且相等的两个角的度数是
90°,90°
.
答案:45°;45°,45°;90°,90°
6. 一个角的补角加上$10^{\circ }$后,等于这个角的余角的3倍,求这个角以及它的余角和补角的度数.
答案:解:设这个角为$x^{\circ }$,则它的余角为$(90-x)^{\circ }$,它的补角为$(180-x)^{\circ }$.根据题意,得$180-x+10=3(90-x)$,解得$x=40$.故这个角为$40^{\circ }$,它的余角为$50^{\circ }$,它的补角为$140^{\circ }$.
7. (2024·宿豫期末)若$∠A和∠B$互补,且$∠A<∠B$,则下列表示$∠A$的余角的式子:①$180^{\circ }-∠A$;②$∠B-90^{\circ }$;③$\frac {1}{2}(∠A+∠B)$;④$\frac {1}{2}(∠B-∠A)$中.其中正确的有(
B
)
A.3个
B.2个
C.1个
D.0个
答案:B
解析:
∵∠A和∠B互补,
∴∠A + ∠B = 180°,∠B = 180° - ∠A。
∠A的余角为90° - ∠A。
①180° - ∠A = ∠B,∠B > 90°(
∵∠A < ∠B,∠A + ∠B = 180°),不是余角,错误。
②∠B - 90° = (180° - ∠A) - 90° = 90° - ∠A,是∠A的余角,正确。
③$\frac{1}{2}(∠A + ∠B)$ = $\frac{1}{2}×180°$ = 90°,不是余角,错误。
④$\frac{1}{2}(∠B - ∠A)$ = $\frac{1}{2}(180° - ∠A - ∠A)$ = 90° - ∠A,是∠A的余角,正确。
正确的有②④,共2个。
B
8. (2024·宿迁新区共同体期末)已知$∠1= 100^{\circ }$,若$∠2和∠1$互补,$∠3和∠2$互余,则$∠3= $
10°
.
答案:10°
解析:
因为∠2和∠1互补,∠1=100°,所以∠2=180°-∠1=180°-100°=80°.
因为∠3和∠2互余,所以∠3=90°-∠2=90°-80°=10°.
10°
9. 若一个角的补角是它的余角的3倍,则这个角的度数为
45°
.
答案:45°
解析:
设这个角的度数为$x$。
它的补角为$180^\circ - x$,余角为$90^\circ - x$。
由题意得:$180^\circ - x = 3(90^\circ - x)$
解得:$x = 45^\circ$
$45^\circ$